October 20, 2019 23:00

안녕하세요?

저는 이번 글에서 Global Minimum Cut을 찾는 Karger’s algorithm에 대해 설명해보려고 합니다.

Introduction

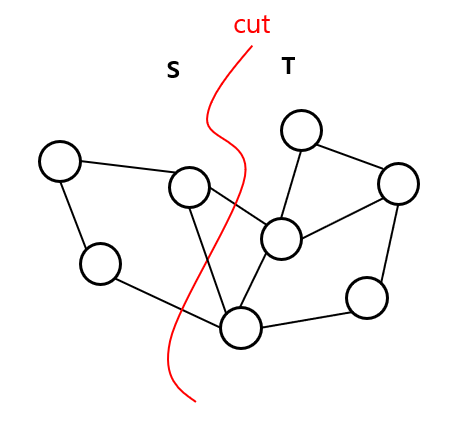
그래프를 두 집합 $S$, $T$로 나누는 것을 그래프의 cut이라고 합니다. 간선에 weight가 있는 그래프에서, 두 점 $s$와 $t$가 주어졌을 때 $s \in S$, $t \in T$를 만족하도록 그래프를 cut하는 상황을 생각해봅시다.

한 쪽 노드는 집합 $S$에, 다른 한 쪽은 $T$에 포함된 모든 edge들의 weight의 합을 cut의 크기라고 합니다. 이 때 크기가 가장 작은 최소 cut은 최대 유량과 같다는 사실(Min-cut Max-flow theorem)은 잘 알려져 있습니다.

따라서 최대 유량을 구하는 여러 알고리즘(Edmond-Karp algorithm, Dinic algorithm 등)을 적용하여, 최소 컷의 크기를 쉽게 구할 수 있습니다.

하지만 두 점 $s$와 $t$가 정해지지 않은, 전체 그래프에서의 global minimum cut을 찾는 것은 어떨까요? 이를 찾는 대표적인 알고리즘으로 determisistic한 Stoer-Wagner Algorithm, 그리고 randomize algorithm인 Karger’s Algorithm이 있습니다.

이번 글에서는 그 중에서 Karger’s algorithm을 소개하도록 하겠습니다.

Karger’s Algorithm

먼저 Karger’s algorithm은 unweighted graph에서 사용이 가능합니다.

사실 Karger’s algorithm은 multigraph에서도 사용이 가능하기 때문에 간선의 u와 v 사이를 잇는 간선의 weight가 w일 때 간선을 w개 만드는 식으로 하면 weighted graph에서도 사용이 가능하지만, 시간복잡도가 그만큼 증가하므로 보통은 unweighted graph를 기준으로 생각합니다.

Karger’s Algorithm은 굉장히 간단한 방식으로 작동합니다.

1. 전체 E개의 edge를 랜덤하게 섞어놓는다.
2. 남은 node의 갯수가 2개가 될 때까지 edge contraction을 진행한다.
3. 남은 2개의 node 사이의 edge의 갯수를 센다. 이는 최솟값의 후보이다.
4. 1번~3번을 충분히 반복하며 최솟값을 찾는다.

Edge contraction은 다음 그림과 같이 두 노드를 합치는 것을 의미합니다.

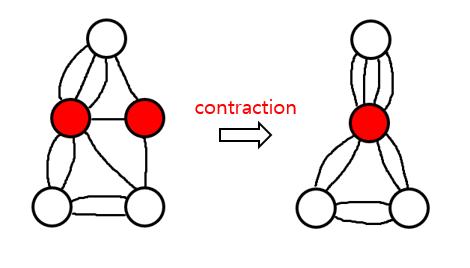
남은 노드의 수가 2개가 될 때까지 edge contraction을 진행하는 것은 disjoint-set 자료구조를 이용하면 $O(E)$ 시간에 작동하도록 구현할 수 있습니다.

그렇다면 이렇게 랜덤하게 고른 순서대로 edge contraction을 진행했을 때, 실제로 global minimum cut에 도달하게 될 확률은 얼마나 될까요? 확률 계산을 위해 먼저 몇 가지 사실을 관찰할 필요가 있습니다.

n개의 node와 E개의 edge를 가진 그래프가 있다고 가정했을 때, 먼저 다음과 같은 사실들이 성립합니다.

1. 각 node에 연결된 edge의 갯수의 총 합은 $2E$이다.
   • 하나의 edge마다 2개의 node와 연결되어 있으므로 자명합니다.
     
2. 그래프의 gloabl minimum cut의 크기는 최대 $\frac{2E}{n}$이다.

• 그래프를 두 집합 S와 T로 분할하되, S에는 1개의 노드 u만 포함하고 T에는 나머지 n - 1개의 노드가 포함되도록 만들어봅시다. 이 때 생기는 cut의 크기는 노드 u에 연결된 edge의 갯수와 동일합니다.

• 모든 n개의 node에 대해 이러한 분할을 만들 수 있으며, 이러한 분할 중 최소 컷의 크기는 각 연결된 edge 수가 가장 적은 node에 연결된 edge 수와 같습니다. 만약 이 값이 $\frac{2E}{n}$보다 크다고 가정하면 node에 연결된 edge의 갯수의 총 합이 2E보다 크게 되므로 1번에 모순입니다. 따라서 이러한 분할 중에는 cut의 크기가 $\frac{2E}{n}$ 이하인 분할이 반드시 존재합니다.

• 위에서 진행한 분할도 모두 valid한 분할이므로, 전체 minimum cut의 크기는 이러한 분할 중의 최솟값보다 같거나 작아야 합니다.
  

1. 하나의 edge를 랜덤하게 골랐을 때, 해당 edge가 minimum cut에 포함된 edge일 확률은 최대 $\frac{2}{n}$이다.

• 2번에서 minimum cut에는 최대 $\frac{2E}{n}$개의 edge만 포함되는 것을 알았으므로, minimum cut에 포함된 edge의 수를 전체 edge의 수로 나누면 됩니다.
  

이제 확률을 계산해봅시다.

맨 처음 edge를 고를 때, 고른 edge가 mincut에 포함되지 않을 확률은 $1 - \frac{2}{n}$입니다. 고른 edge에 대해 edge contraction을 진행하면 n - 1개의 node들만 남게 되는데, 이 중에서 또 edge를 골랐을 때 해당 edge가 mincut에 포함되지 않을 확률은 $1 - \frac{2}{n - 1}$입니다.

edge를 고르는 과정에 node 2개가 남을 때까지 반복되므로, 알고리즘이 종료될 때까지 진행하였을 때 모든 edge가 mincut에 포함되지 않을 확률은 다음과 같이 계산됩니다.

$(1 - \frac{2}{n}) \times (1 - \frac{2}{n - 1}) \times … \times (1 - \frac{2}{4}) \times (1 - \frac{2}{3})$

$= \frac{n - 2}{n} \times \frac{n - 3}{n - 1} \times … \times \frac{2}{4} \times \frac{1}{3}$

$= \frac{2}{n(n - 1)}$

즉, 2개의 node가 남을 때까지 contraction을 진행했을 때 올바른 minimum cut이 찾아질 확률은 $\frac{2}{n(n - 1)}$입니다. 굉장히 작은 확률이지요.

하지만 알고리즘의 반복 횟수를 충분히 늘린다면, 올바른 minimum cut을 찾을 확률은 점차 증가합니다. 과연 몇 번이나 반복해야 할까요?

알고리즘을 T번 반복한다고 가정했을 때, 올바른 minimum cut을 찾지 못할 확률은 다음과 같이 계산할 수 있습니다.

$(1 - \frac{2}{n(n - 1)})^T$

이 때 $T = n^2 \ln{n}$으로 잡으면, 올바른 minimum cut을 찾지 못할 확률이 $\frac{1}{n}$ 미만이 됨을 보일 수 있습니다.

이는 $1 - x \le e^{-x}$라는 식을 이용하면 쉽게 계산 가능합니다. $$(1 - \frac{2}{n(n - 1)})^{n^2 \ln{n}} < (1 - \frac{1}{n^2})^{n^2 \ln{n}}
\le (e^{- \frac{1}{n^2}})^{n^2 \ln{n}} = \frac{1}{e^{\ln{n}}} = \frac{1}{n}$

이 때의 시간 복잡도는 $O(En^2 \log{n})$이 됩니다.

보통 edge의 갯수는 노드의 수의 제곱에 비례하므로, Karger’s algorithm의 시간복잡도는 $O(n^4 \log{n})$입니다. 이는 n이 100 정도만 되어도 오랜 시간이 걸릴 정도의 복잡도입니다.

Complete graph에서 Karger’s algorithm을 이용해 global minimum cut을 찾는 과정을 C++ 코드로 작성해보았습니다.

#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;

int p[10000];

int find(int i) {
	if (i == p[i]) return i;
	return p[i] = find(p[i]);
}

void merge(int a, int b) {
	a = find(a); b = find(b);
	if (a != b) p[a] = b;
}

int main() {
	srand(time(NULL));

	int n = 50;
	int e = 0;
	vector<pair<int, int>> edge;
	for (int i = 0; i < n; ++i) {
		for (int j = i + 1; j < n; ++j) {
			e++;
			edge.push_back({i, j});
		}
	}

	int REPEAT = n * n * log(n);

	int ans = e;
	for (int rep = 0; rep < REPEAT; ++rep) {
		for (int i = 0; i < n; ++i) p[i] = i;		
		random_shuffle(edge.begin(), edge.end());

		int cnt = n;
		int connect = 0;

		for (int i = 0; i < e; ++i) {
			int u = edge[i].first;
			int v = edge[i].second;
			if (cnt == 2) {
				for (int j = i; j < e; ++j) {
					int uu = edge[j].first;
					int vv = edge[j].second;
					if (find(uu) != find(vv)) connect++;
				}
				break;
			}
			u = find(u); v = find(v);
			if (u != v) {
				cnt--;
				p[u] = v;
			}
		}

		ans = min(ans, connect);
	}
	cout << ans << endl;
}

Karger–Stein algorithm

Karger-stein algorithm은 Karger algorithm을 조금 더 보완한 형태의 알고리즘입니다.

Karger 알고리즘에서 확률을 구하는 부분을 다시 한 번 살펴봅시다.

처음에 edge를 고를 때에는 minimum cut에 속하는 edge를 고를 확률이 $\frac{2}{n}$ 정도로 그리 크지 않습니다. 하지만 node의 갯수가 점차 감소할수록 minimum cut에 속하는 edge를 선택할 확률이 점점 높아져, 최종적으로 $2 / 3$까지 높아집니다.

Karger-Stein algorithm은 이러한 점에 착안하였습니다. Minimum cut에 속할 확률이 $\frac{1}{2}$이 될 때까지만 진행하고, 확률이 $\frac{1}{2}$이 될 때마다 검토하는 횟수를 2배로 늘려준 후 그 중 최솟값을 찾습니다.

구체적으로 알고리즘의 진행 과정은 다음과 같습니다. Sudo코드로 작성하였습니다.

def contract(G = (V, E), t):
	while |V| > t:
		randomly choose one edge
		G = G - {e}
	return G

def fastmincut(G = (V, E)):
	if |V| < 6:
		return BFmincut(G)
	else:
		t = ceil(1 + |V| / sqrt(2))
		G1 = contract(G, t)
		G2 = contract(G, t)
		return min(fastmincut(G1), fastmincut(G2))

먼저 V의 크기가 일정 수준 이하로 작을 때에는, Brute force로 모든 경우의 수를 따져보며 mincut을 찾습니다.

그렇지 못한 경우에는, node의 갯수가 t = ceil(1 + |V| / sqrt(2))개가 될 때까지 각각 다른 contraction을 2번 진행해줍니다. 해당 t가 선택된 이유는, Minimum cut에 속할 확률이 $\frac{1}{2}$을 넘는 수이기 때문입니다.

contraction을 통해 더 작은 크기의 그래프 2개가 만들어지면, 재귀적으로 mincut을 찾는 것을 반복하며 그 중 작은 값을 return합니다.

그렇다면 해당 알고리즘이 옳게 작동할 확률을 구해봅시다.

알고리즘이 옳은 minimum cut을 찾으려면 먼저 contraction 과정에서 minimum cut에 속하는 edge들이 제거되지 않아야 하며(t까지 진행하므로 확률은 $\frac{1}{2}$입니다), 생성된 더 작은 크기의 그래프에서 재귀적으로 진행되는 과정 또한 minimum cut에 속하는 edge들을 제거하지 않아야 합니다.

이러한 과정이 2회 반복되므로, 알고리즘이 정확한 mincut을 구할 확률은 다음과 같은 점화식으로 나타내집니다.

$P(n) = 1 - (1 - \frac{1}{2} P(1 + \frac{n}{\sqrt{2}}))^2$

위 점화식을 풀면 $P(n) = \Omega (\frac{1}{\log{n}})$라는 값을 얻게 됩니다. 이 값이 fastmincut 함수를 한 번 실행시킬 때의 정확도입니다.

시간복잡도도 한 번 살펴보겠습니다.

fastmincut 함수를 한 번 실행할 때, 재귀적으로 실행되는 점화식은

$T(n) = 2 T(1 + \frac{n}{\sqrt{2}}) + O(n^{2})$

로 나타낼 수 있습니다.

이 점화식을 풀면 $T(n) = O(n^{2} \log{n})$이 됨을 알 수 있습니다.

이 값이 fastmincut 함수를 한 번 실행시킬 때의 시간 복잡도입니다.

Karger’s algorithm과 같이 정확도의 기댓값을 $\frac{1}{n}$으로 맞추려면 최소 $O(\frac{\log{n}}{P(n)}) = \log^{2}{n}$번 함수를 실행시켜야 합니다. 따라서 알고리즘의 총 시간복잡도는 $O(n^{2}\log^3{n})$이 됩니다. $O(n^4 \log{n})$이던 Karger’s algorithm보다 시간복잡도가 훨씬 더 줄어들었습니다.

아래는 C++로 구현된 코드입니다. 그래프를 재귀적으로 호출하는 과정에서 overhead가 꽤 커서 생각만큼 빠르게 동작하지는 않았습니다.

#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;

struct Graph {
	int find(int i) {
		if (i == p[i]) return i;
		return p[i] = find(p[i]);
	}	
	vector<int> p;
	vector<pair<int, int>> edge;
	int size;
};

int fastKarger(Graph& g) {
	if (g.size < 6) {
		int ret = g.edge.size();
		for (int i = 1; i < (1 << g.size) - 1; ++i) {
			int connect = 0;
			for (int j = 0; j < g.edge.size(); ++j) {
				int u = g.edge[j].first;
				int v = g.edge[j].second;
				if (((i & (1 << u)) == 0) != ((i & (1 << v)) == 0)) connect++;
			}
			ret = min(ret, connect);
		}
		return ret;
	}
	else {
		Graph gNew[2];
		int t = 1 + g.size / sqrt(2);
		for (int rep = 0; rep < 2; ++rep) {
			int cnt = g.size;
			for (int i = 0; i < g.size; ++i) g.p[i] = i;
			random_shuffle(g.edge.begin(), g.edge.end());
			for (int i = 0; i < g.edge.size(); ++i) {
				int u = g.edge[i].first;
				int v = g.edge[i].second;
				if (cnt <= t) {
					vector<int> reindex(g.size);
					int counter = 0;
					for (int j = 0; j < g.size; ++j) {
						if (g.p[j] == j) reindex[j] = counter++;
					}
					gNew[rep].p.resize(t);
					for (int j = 0; j < t; ++j) gNew[rep].p[j] = j;
					for (int j = i; j < g.edge.size(); ++j) {
						int uu = g.find(g.edge[j].first);
						int vv = g.find(g.edge[j].second);
						if (uu != vv) {
							gNew[rep].edge.push_back({reindex[uu], reindex[vv]});
						}
					}
					break;
				}
				u = g.find(u); v = g.find(v);
				if (u != v) {
					cnt--;
					g.p[u] = v;
				}
			}
			gNew[rep].size = t;
		}
		return min(fastKarger(gNew[0]), fastKarger(gNew[1]));
	}
}

int main() {
	srand(time(NULL));

	int n = 100;

	Graph g;
	g.p.resize(n);
	for (int i = 0; i < n; ++i) g.p[i] = i;
	g.size = n;
	for (int i = 0; i < n; ++i) {
		for (int j = i + 1; j < n; ++j) {
			g.edge.push_back({i, j});
		}
	}

	int REPEAT = log(n) * log(n);

	int ans = g.edge.size();
	for (int rep = 0; rep < REPEAT; ++rep) {
		ans = min(ans, fastKarger(g));
	}

	cout << ans << endl;
}

Conclusion

알고리즘 문제를 풀 때 randomize algorithm을 사용하는 것은 사실상 최후의 수단이지만, Karger’s algorithm과 같이 몇몇 randomize algorithm은 적절한 시간 복잡도 내에서 꽤 높은 확률로 정답을 얻어낼 수 있습니다.

이러한 흥미로운 알고리즘을 한 번쯤 공부해보는 것은 아주 재미있는 경험이 될 것이라 생각합니다.

감사합니다.

Reference

Karger’s algorithm wikipedia

A New Approach to the Minimum Cut Problem