Mo's Algorithm on Trees
이 게시글은 LCA(lowest common ancestor)에 대한 지식이 선행되어야 하지만 본 글에서는 소개하지 않습니다.
Mo’s Algorithm이란?
Mo’s algorithm은 평방 분할(sqrt decomposition)의 일종의 활용 기법으로, 오프라인으로 구간 쿼리 문제를 해결할 때 사용할 수 있습니다. 이미 이에 관한 좋은 글이 있어 (링크)로 대체하겠습니다.
Mo’s Algorithm on Trees?
위 Mo’s Algorithm을 Tree에서 하는 것을 의미합니다. Mo’s는 앞서 말씀드렸던 것처럼 구간 쿼리 문제를 해결할 때 쓰이기 때문에 트리에서의 쿼리를 구간 쿼리처럼 나타낼 필요가 있는데요. 이를 Euler Tour on Trees를 이용하여 해결할 수 있습니다. 트리의 루트에서 DFS를 시행하였을 때, 방문한 간선의 번호를 순서대로 나열한 수열을 봅시다. 이때, 어느 트리의 서브노드를 전부 방문하고 부모로 올라가는 과정도 포함합니다.

위 그림에서는 5-6-6-4-4-5-7-3-3-7-2-2가 그중 하나가 됩니다. 이를 조금 변형하여 간선이 아닌 노드에 번호를 붙이고, 어떤 노드를 방문한 첫 번째 순간과 마지막 순간을 순서대로 나열하는 것을 생각해봅시다. 위 그림을 아래 그림처럼 표현한 다음에 순서를 나열해보면,
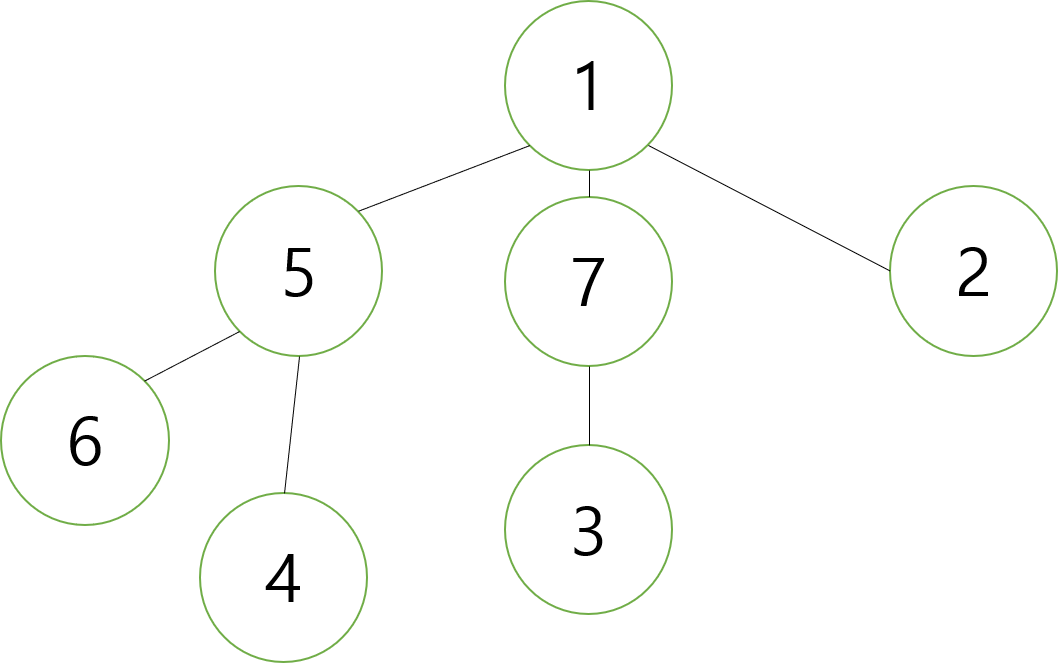
1-5-6-6-4-4-5-7-3-3-7-2-2-1로 시작과 끝에 루트 노드 1을 추가한 형태가 됩니다. 이때 수열에서 같은 수(노드) 두개로 둘러싸인 구간은 해당 노드의 서브노드만 전부 2번씩 포함한 형태가 됩니다. 즉, 어느 서브트리를 하나의 구간으로 표현할 수 있게 됐습니다.
위 수열을 구하는 간단한 코드입니다.
void EulerTour(int node) {
printf("%d ", node);
for (int i : child[node])
EulerTour(i);
printf("%d ", node);
}
그러면 수열 1-5-6-6-4-4-5-7-3-3-7-2-2-1에서 같은 수 두개로 둘러싸인 구간을 모두 구해볼까요?
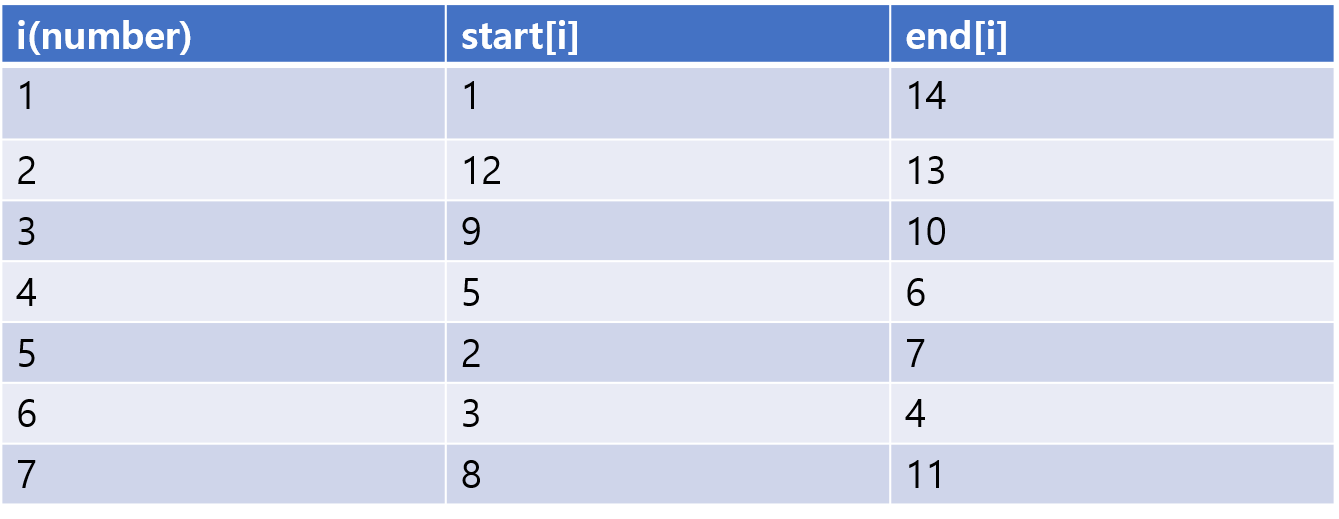
이렇게 나타낼 수 있겠죠. 우리는 이제 서브트리를 구간으로 표현할 수 있으므로 트리에서 MO’s Algorithm을 이용하여 서브트리 쿼리를 해결할 준비가 전부 되었습니다. 아래 문제를 해결해봅시다.
$N(1 \leq N \leq 10^5)$개 정점을 가진 a rooted tree가 주어진다. 각 정점에는 임의의 수 $A_i(1 \leq A_i \leq 10^6)$가 부여되어 있다. 이때, $Q(1 \leq Q \leq 10^5)$개의 쿼리를 해결하시오.
- $Query\space x$ : $x$의 서브트리에 속한 정점들에 존재하는 서로 다른 수의 개수를 출력한다.
이 문제는 수열과 쿼리5를 서브트리 버전으로 바꾼 것입니다.
$Query\space x$는 $start[x]$~$end[x]$ 구간에 존재하는 정점이 가진 서로 다른 수의 개수를 세는 것과 같습니다. 그래서 EulerTour로 수열을 만들고, 각 정점의 $start$와 $end$를 기록하면 기존의 문제와 같은 방법으로 해결할 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
int num[100000]; // 배열 A
int st[100000], ed[100000]; // start, end
int cnt[1000001]; // cnt[i] : i의 개수
vector<int> child[100000];
vector<int> seq; // sequence
int ret = 0, sqrtN;
int ans[100000]; // 쿼리의 정답 저장
struct query {
int l, r, id;
} qry[100000];
void EulerTour(int o) {
st[o] = seq.size();
seq.push_back(num[o]);
for (int i : child[o]) EulerTour(i);
ed[o] = seq.size();
seq.push_back(num[o]);
}
void add(int i) {
if (++cnt[seq[i]] == 1) ret++;
}
void erase(int i) {
if (--cnt[seq[i]] == 0) ret--;
}
int main() {
int n, q;
scanf("%d %d", &n, &q);
for (int i = 0; i < n; i++) scanf("%d", &num[i]);
int a, b;
for (int i = 0; i < n - 1; i++) {
scanf("%d %d", &a, &b);
a--; b--;
child[a].push_back(b);
}
EulerTour(0); // root : 0
sqrtN = sqrt(seq.size());
for (int i = 0; i < q; i++) {
scanf("%*s %d", &a);
a--;
qry[i] = {st[a], ed[a], i}; // a의 서브트리를 st[a] ~ ed[a]로 표현
}
// 이하 모스 알고리즘 적용.
sort(qry, qry + q, [](query a, query b){
if (a.r / sqrtN == b.r / sqrtN) return a.l < b.l;
return a.r < b.r;
});
int pl = qry[0].l, pr = qry[0].l - 1;
for (int i = 0; i < q; i++) {
for (int j = pr + 1; j <= qry[i].r; j++) add(j);
for (int j = pl - 1; j >= qry[i].l; j--) add(j);
for (int j = pr; j > qry[i].r; j--) erase(j);
for (int j = pl; j < qry[i].l; j++) erase(j);
pl = qry[i].l, pr = qry[i].r;
ans[qry[i].id] = ret;
}
for (int i = 0; i < q; i++)
printf("%d\n", ans[i]);
}
위 문제를 해결하는 코드입니다.
서브트리 쿼리뿐만 아니라 경로 쿼리에도 적용할 수 있는데요. 아래 문제를 봅시다.
$N$개 정점을 가진 a rooted tree가 주어진다. 각 정점에는 임의의 수 $A_i$가 부여되어 있다. 이때, $Q$개의 쿼리를 해결하시오.
- $Query\space a\space b$ : 정점 $a$와 $b$를 잇는 경로에 속한 정점들에 존재하는 서로 다른 수의 개수를 출력한다.
마찬가지로 임의의 경로를 Euler tour sequence의 구간으로 정의해봅시다.
$p = lca(a, b)$라고 할 때,
$Case 1: if(p = a)$
이 경우 $start[a]$~$start[b]$ 구간으로 경로를 표현할 수 있습니다. 경로에 존재하지 않는 정점은 이 구간 내에서 2번 혹은 0번 등장하게 되며 구간에서 정확히 한 번씩 등장하는 정점과 경로상의 정점은 일치합니다.
$Case 2: if(p\space \neq a)$
$end[a]$~$start [b]$ 구간에 정점 $p$를 따로 계산하면 경로를 표현할 수 있습니다. 마찬가지로, 구간 내에 정확히 한 번씩 등장하는 정점들만 경로에 포함됩니다. $p$는 구간에 포함되지 않지만 경로에 포함되는 유일한 정점이므로 따로 고려해야 합니다.
위 두 가지 경로를 모두 구간으로 표현함에 따라 우리는 경로 쿼리도 Mo’s Algorithm으로 해결할 준비가 되었습니다.
Count on a tree(링크)
앞서 설명한 문제와 동일한 문제입니다. 이 문제를 해결하는 코드를 끝으로 글을 마치겠습니다.
감사합니다.
#include <bits/stdc++.h>
using namespace std;
int num[40000]; // 배열 A
int st[40000], ed[40000]; // start, end
int cnt[40000]; // cnt[i] : i의 개수
int dist[40000], spa[40000][17]; // LCA를 찾기 위함
char on[40000]; // 해당 정점이 현재 구간에 속해있다면 1, 아니면 0
vector<int> edge[40000], x; // x : 좌표압축 위함
vector<int> seq; // sequence
int ret = 0, sqrtN;
int ans[100000]; // 쿼리의 정답 저장
struct query {
int l, r, lca, id;
} qry[100000];
void EulerTour(int o, int parent, int depth) {
st[o] = seq.size();
seq.push_back(o);
dist[o] = depth; spa[o][0] = parent;
for (int i = 1; i < 17; i++)
spa[o][i] = spa[spa[o][i - 1]][i - 1];
for (int i : edge[o]) if (i != parent)
EulerTour(i, o, depth + 1);
ed[o] = seq.size();
seq.push_back(o);
}
int get_lca(int a, int b) {
if (dist[a] > dist[b]) swap(a, b);
for (int i = 16; i >= 0; i--)
if (dist[a] <= dist[spa[b][i]])
b = spa[b][i];
if (a == b) return a;
for (int i = 16; i >= 0; i--)
if (spa[a][i] != spa[b][i])
a = spa[a][i], b = spa[b][i];
return spa[a][0];
}
void update(int i) {
on[i] ^= 1;
if (on[i] && ++cnt[num[i]] == 1) ret++;
else if (!on[i] && --cnt[num[i]] == 0) ret--;
}
int main() {
int n, q;
scanf("%d %d", &n, &q);
for (int i = 0; i < n; i++) {
scanf("%d", &num[i]);
x.push_back(num[i]);
}
sort(x.begin(), x.end());
x.erase(unique(x.begin(), x.end()), x.end());
for (int i = 0; i < n; i++)
num[i] = lower_bound(x.begin(), x.end(), num[i]) - x.begin();
// num[i]를 좌표압축.
int a, b;
for (int i = 0; i < n - 1; i++) {
scanf("%d %d", &a, &b);
a--; b--;
edge[a].push_back(b);
edge[b].push_back(a);
}
EulerTour(0, 0, 0);
sqrtN = sqrt(seq.size());
for (int i = 0; i < q; i++) {
scanf("%d %d", &a, &b);
a--; b--;
if (st[a] > st[b]) swap(a, b);
int lca = get_lca(a, b);
if (lca == a) qry[i] = {st[a], st[b], -1, i};
else qry[i] = {ed[a], st[b], lca, i};
}
sort(qry, qry + q, [](query a, query b){
if (a.r / sqrtN == b.r / sqrtN) return a.l < b.l;
return a.r < b.r;
});
int pl = qry[0].l, pr = qry[0].l - 1;
for (int i = 0; i < q; i++) {
for (int j = pr + 1; j <= qry[i].r; j++) update(seq[j]);
for (int j = pl - 1; j >= qry[i].l; j--) update(seq[j]);
for (int j = pr; j > qry[i].r; j--) update(seq[j]);
for (int j = pl; j < qry[i].l; j++) update(seq[j]);
pl = qry[i].l, pr = qry[i].r;
if (qry[i].lca != -1) update(qry[i].lca);
ans[qry[i].id] = ret;
if (qry[i].lca != -1) update(qry[i].lca);
}
for (int i = 0; i < q; i++)
printf("%d\n", ans[i]);
}
이 게시글은 https://codeforces.com/blog/entry/43230를 참고하여 작성되었습니다.