Segment의 개수를 이용하는 순열 경우의 수 문제
소개
특정 조건을 만족하는 순열의 개수를 세는 문제 중에서, segment(이하 구간)의 개수를 이용하는 특이한 꼴의 다이나믹 프로그래밍 문제를 다뤄보려고 합니다. 예시 문제를 통해 살펴봅시다.
문제1. 길이가 $N$, Increasing segment의 개수가 $K$개인 순열의 개수
Increasing segment란, $l+1 \leq i \leq r$인 모든 $i$에 대해 $A_{i-1} < A_i$를 만족하는 $[l, r]$이라고 합니다. 단, 다른 increasing segment에 포함되는 구간은 무시하는 걸로 합시다.
예를 들어, $1\space4\space5\space2\space3\space6\space8\space7$의 increasing segment는 $[1, 3], [4, 7], [8, 8]$로 총 3개입니다.
우리는 길이가 $N$이고 increasing segment의 개수가 $K$개인 순열의 개수를 구하려고 합니다. 이 문제는 어떻게 해결할 수 있을까요? 이 문제는 다이나믹 프로그래밍을 이용하여, $O(NK)$에 해결할 수 있습니다. $D_{n,k}$를 길이가 $n$이고 수 $1 \sim n$만을 사용하며, increasing segment의 개수가 $k$개인 순열의 개수라고 합시다. 위의 $(n, k)$를 가지는 임의의 순열에서 $n+1$이라는 수를 임의의 자리에 추가한다고 생각해 봅시다. 경우의 수는 크게 아래와 같이 4가지로 분류할 수 있습니다.

- $n+1$을 넣으려는 위치의 왼쪽 값이 오른쪽보다 큰 경우입니다. 이 경우 increasing segment의 개수가 증가하지 않습니다.
- $n+1$을 넣으려는 위치의 왼쪽 값이 오른쪽보다 작은 경우입니다. 이 경우 increasing segment의 개수가 증가합니다.
- $n+1$을 순열의 맨 왼쪽에 넣는 경우입니다. 이 경우 increasing segment의 개수가 증가합니다.
- $n+1$을 순열의 맨 오른쪽에 넣는 경우입니다. 이 경우 increasing segment의 개수가 증가하지 않습니다.
increasing segment의 개수를 증가시키지 않는 1번 경우는 $k-1$개, 4번 경우는 1개로 총 $k$개의 경우가 존재합니다. increasing segment의 개수를 증가시키는 경우는 $n+1-k$개일 것입니다. 따라서, 아래와 같은 상태 변화를 얻을 수 있습니다.
$D_{1,1} = 1$
$D_{n,k} \times k \Rightarrow D_{n+1, k}$
$D_{n,k} \times (n+1-k) \Rightarrow D_{n+1, k+1}$
이 점화식을 이용하면 우리는 최종적으로 $D_{N,K}$를 $O(NK)$만에 구하며 문제를 해결할 수 있습니다.
문제2. Kangaroo(링크)
위치 $1 \sim N$이 있습니다. 캥거루가 $cs$에서 출발하여 모든 위치를 정확히 한 번씩 방문하여 $cf$에서 마무리하는 경우의 수를 구하는 문제입니다. 단, 캥거루의 직전 위치를 $prev$, 현재 위치를 $current$, 다음 위치를 $next$라고 할 때, $prev < current$라면, $current > next$
$prev > current$라면, $current < next$를 만족해야 합니다.
시작점과 끝점이 정해져 있어서 무척 어렵게 느껴집니다. 이 문제도 마찬가지로 segment의 개수가 포함된 점화식으로 문제를 해결할 수 있습니다. 캥거루가 이동한 경로는 하나의 순열일 것입니다. 아래 그림을 봅시다.
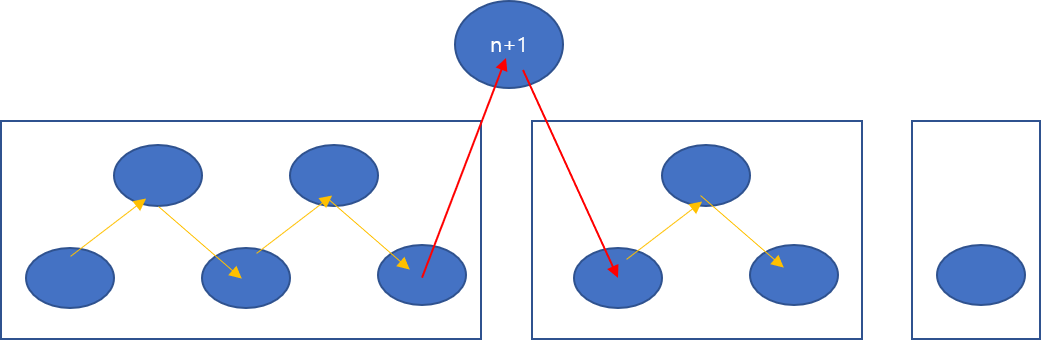
한 직사각형 내부의 모습처럼 캥거루가 이동한 위치는 커졌다 작아졌다를 반복하는 형태일 것입니다. 위 그림의 하나의 직사각형처럼 양쪽 끝이 아래로 내려가 있는 형태의 경로를 하나의 “구간”으로 정의해봅시다. 위 그림에서 구간의 개수는 3개입니다.
$D_{n,k}$를 길이가 $n$이고 수 $1 \sim n$만을 사용하며, 위와 같은 구간의 개수가 $k$개인 순열의 개수라고 합시다.
위의 $(n, k)$를 만족하는 임의의 순열에서 $n+1$이라는 수를 임의의 자리에 추가한다고 해봅시다. 위 그림과 같이 $n+1$을 두 구간의 사이에 넣는다면, 두 구간은 하나로 합쳐지게 됩니다. 그 외의 위치는 구간을 하나 증가시키게 됩니다.
이와 같은 상태 변화를 표현하면,
$D_{n,k} \times (k-1) \Rightarrow D_{n+1,k-1}$
$D_{n,k} \times ((n+1)-(k-1)) \Rightarrow D_{n+1,k+1}$입니다.
시작과 끝 위치는 $cs$와 $cf$로 정해져 있으므로 $n+1$이 $cs$ 혹은 $cf$인 경우는 구간의 개수를 1개 증가시키면서 맨 앞 혹은 맨 뒤에 배치될 것입니다. 따라서, 이 경우를 표현하면 아래와 같습니다.
$D_{n,k} \Rightarrow D_{n+1,k+1}$
아쉽게도, 우리가 찾은 식은 약간 부족합니다.
첫째로, 시작 혹은 끝이 배치된 순간부터 양 끝 자리에는 수를 추가할 수 없으므로 경우에서 제외해야 합니다.
둘째로, 정답을 $D_{N,1}$이라고 하고 싶지만 양 끝 자리가 길이 1인 구간에 속하는 경우도 올바른 경우의 수에 포함해야 합니다.
따라서, 함수 $D$의 정의를 살짝 바꿔봅시다.
$D_{n,k.c}$를 길이가 $n$이고 수 $1 \sim n$만을 사용하며, 위와 같은 구간의 개수가 $k$개면서, 길이가 1인 구간을 이루고 있는 $cs$ 혹은 $cf$의 개수가 $c$개인 순열의 개수라고 합시다. 그러면, 정답은 $D_{N,1,0} + D_{N,2,1} + D_{N,3,2}$가 됩니다.
아래는 앞서 언급한, 두 가지 문제점에 대해서 식을 적절히 수정하여 작성한 코드입니다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
ll dp[2001][2001][3];
int main() {
int n, s, e;
scanf("%d %d %d", &n, &s, &e);
int ff = 0;
dp[1][1][0] = 1;
for (int i = 1; i < n; i++) {
if (i == s || i == e) ff++; // 넣을 수 없는 양끝에 대한 표시.
for (int j = 1; j <= i; j++)
for (int k = 0; k < 3; k++) {
ll me = dp[i][j][k];
if (i + 1 == s || i + 1 == e) {
// i+1이 cs 혹은 cf인 경우.
if (k < 2) dp[i + 1][j + 1][k + 1] = (dp[i + 1][j + 1][k + 1] + me) % MOD;
}
else {
// 양끝의 길이 1짜리 구간을 합치지 않으면서, 두 구간을 합치는 경우.
dp[i + 1][j - 1][k] = (dp[i + 1][j - 1][k] + me * (j - 1 - k)) % MOD;
// 양끝의 길이 1짜리 구간을 포함하여 두 구간을 합치는 경우.
if (k) dp[i + 1][j - 1][k - 1] = (dp[i + 1][j - 1][k - 1] + me * k) % MOD;
// 하나의 구간을 두개로 분리하는 경우.
dp[i + 1][j + 1][k] = (dp[i + 1][j + 1][k] + me * (i + 1 - ff - (j - 1))) % MOD;
}
}
}
printf("%lld", (dp[n][1][0] + dp[n][2][1] + dp[n][3][2]) % MOD);
}
문제3. 기묘한 여행계획(링크)
문제 조건에 의해서, $a < b$인 $a, b$에 대해, 두 여행지 $a$와 $b$ 사이를 이동하는 비용은 $(X_b + Y_b) - (X_a + Y_a)$가 됩니다. 따라서, 비용을 계산할 때, $X_i$, $Y_i$ 개별적인 값보다는 $X_i + Y_i$ 값이 중요하므로 이를 $C_i$로 다시 표현합시다. 앞선 문제들과 마찬가지로, 창수의 이동 경로는 하나의 순열로 표현이 됩니다. 구간의 개수와 다이나믹 프로그래밍으로 문제를 해결해봅시다. 여태까지 $1 \sim n$번 여행지의 상대적인 순서를 정했을 때, 최종 경로에서 순서가 인접해 있는 여행지들을 묶어 하나의 “구간”이라고 해봅시다. 그리고 아래와 같은 함수를 정의해봅시다.
$D_{n,k,b,c}$를 $1 \sim n$번 여행지 간의 순서를 정했고, $k$개의 구간이 있고, 경로의 출발지와 도착지로 $c$개를 배정한 상태를 $b$원에 만드는 경우의 수라고 해봅시다.

위 그림에서 하나의 직사각형으로 묶인 여행지들은 최종 순서에서도 인접해 있는 여행지로. 각 직사각형을 하나의 구간이라고 합시다. 또, 주황색으로 칠해진 점은 출발지 혹은 도착지(끝점)라고 합시다. 그러면 이 그림은 $(7, 4, b, 1)$로 표현이 됩니다. 우리가 구해야 하는 정답은 최종적으로 $D_{N, 1, B이하인 값, 2}$가 될 것입니다.
위의, $(n, k, b, c)$를 가지는 상태에서 $n+1$번 여행지를 임의의 위치에 추가한다고 생각해 봅시다. 크게 5가지의 경우로 나눌 수 있습니다.
-
끝점이 아니면서, 어떤 한 구간과 인접하게 배정하는 경우. $2 \times k - c$개의 경우가 있을 것입니다. 이 경우, $n+1$번 여행지는 최종적으로 본인보다 작은 번호의 여행지 하나, 큰 번호의 여행지 하나와 인접하게 됩니다.
-
두 구간에 동시에 인접하게 배정하는 경우. $k - 1$개의 경우가 있을 것입니다. 이 경우, 해당 여행지는 최종적으로 본인보다 작은 번호의 여행지 두 개와 인접하게 됩니다. 또한, 구간의 개수가 하나 줄어듭니다.
-
끝점이 아니면서, 어떤 구간과도 인접하지 않게 배정하는 경우. $k + 1 - c$개의 경우가 있을 것입니다. 이 경우, 해당 여행지는 최종적으로 본인보다 큰 번호의 여행지 두 개와 인접하게 됩니다. 또한, 구간의 개수가 하나 증가합니다.
-
끝점이면서, 어떤 구간과 인접한 위치에 배정하는 경우. $2 - l$개의 경우가 있을 것입니다. 이 경우, 해당 여행지는 최종적으로 본인보다 작은 번호의 여행지 하나와 인접하게 됩니다. 또한, 끝점의 개수가 하나 증가합니다.
-
끝점이면서, 어떤 구간과도 인접하지 않게 배정하는 경우. $2 - l$개의 경우가 있을 것입니다. 이 경우, 해당 여행지는 최종적으로 본인보다 큰 번호의 여행지 하나와 인접하게 됩니다. 또한, 구간의 개수와 끝점의 개수가 하나 증가합니다.
5가지 경우 중 $n+1$번 여행지를 어떤 경우에 배치하냐에 따라서, $n+1$번과 인접하게 되는 여행지 번호와의 대소 관계가 정해지므로, $C_{n+1}$이 $b$에 기여하게 되는 양 또한 정해집니다. 이것을 그대로 구현하면, $O(N \times N \times NB)$의 시간 복잡도로 문제를 제한 시간 내에 해결하기에는 약간 느립니다.
조금 더 나아가봅시다. 현재 상태에서, 구간과 인접한 곳 중 아직 배정되지 않은 $2 \times k - c$개의 자리는 나중에 항상 자신보다 작은 번호의 여행지와 인접하게 됩니다. 따라서, $n+1$을 배정할 때, $2 \times k - c$개의 자리만큼 확정적으로 $C_{n+1} - C_{n}$만큼의 비용이 더 필요하게 됩니다. 따라서, $b$를 계산하는 부분에서 뺄셈을 없앨 수 있게 되어서 문제를 $O(N^2B)$에 해결할 수 있습니다.
위 로직을 구현한 코드입니다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int MOD = 1000000007;
int n, b;
pii vec[61];
int dp[61][61][2001][3], val[61];
int main() {
scanf("%d %d", &n, &b);
for (int i = 1; i <= n; i++) {
scanf("%d %d", &vec[i].first, &vec[i].second);
val[i - 1] = vec[i].first + vec[i].second - vec[i - 1].first - vec[i - 1].second;
}
if (n == 1) return !printf("1"); // 시작점과 끝점이 같은 유일한 반례
dp[1][1][0][0] = 1;
dp[1][1][0][1] = 2;
for (int i = 1; i < n; i++)
for (int j = 1; j <= i; j++)
for (int k = 0; k <= b; k++)
for (int l = 0; l < 3; l++) {
ll co = (j * 2 - l) * val[i] + k;
if (co > b) continue;
ll me = dp[i][j][k][l];
// 구간을 새로 만드는 경우.
dp[i + 1][j + 1][co][l] = (dp[i + 1][j + 1][co][l] + me * (j + 1 - l)) % MOD;
// 기존 구간 하나에 붙이는 경우.
dp[i + 1][j][co][l] = (dp[i + 1][j][co][l] + me * (j * 2 - l)) % MOD;
// 두 구간을 합치는 경우.
dp[i + 1][j - 1][co][l] = (dp[i + 1][j - 1][co][l] + me * (j - 1)) % MOD;
// 지금 넣는 점이 끝점인 경우.
if (l < 2) {
// 구간을 새로 만드는 경우.
dp[i + 1][j + 1][co][l + 1] = (dp[i + 1][j + 1][co][l + 1] + me * (2 - l)) % MOD;
// 기존 구간 하나에 붙이는 경우.
dp[i + 1][j][co][l + 1] = (dp[i + 1][j][co][l + 1] + me * (2 - l)) % MOD;
}
}
ll ans = 0;
for (int i = 0; i <= b; i++) ans += dp[n][1][i][2];
printf("%lld", ans % MOD);
}
마치며
순열에서 segment의 개수라는 특이한 상태 정의가 필요한 다이나믹 프로그래밍 문제들을 풀어봤습니다. 궁금하신 점이나 잘못된 부분이 있다면, 제 블로그(링크)를 통해 전달하실 수 있습니다.
읽어주셔서 감사합니다.