Queue Undo Trick
개요
최근에 소개된 아이디어라 한글 자료가 없어서 글을 작성하게 되었습니다.
자료구조의 업데이트 연산이 Amortized 시간복잡도를 갖지 않는다면 가장 최근에 한 업데이트를 취소하는 롤백 연산도 같은 시간복잡도에 구현할 수 있음이 알려져 있습니다.
이 글에서는 롤백 연산의 아이디어를 활용한, 가장 오래된 업데이트를 취소하는 Queue-Undo 연산에 대해 소개합니다. 이 연산은 기존의 Offline Dynamic Connectivity 알고리즘과는 달리 온라인으로 동작한다는 장점을 가지고 있습니다.
유니온-파인드 자료구조에 Queue-Undo 연산을 구현해서 연습 문제들을 해결할 것이기 때문에, 사전 지식으로 유니온 파인드를 알고 있음을 가정하고 진행하겠습니다.
롤백 연산
롤백 연산을 구현하면 Amortized 시간복잡도가 깨지므로 path compression은 사용하지 않고, union by rank만을 사용합니다. Union 연산을 할 때 배열의 몇몇 값들이 바뀔 텐데, 변화가 있었던 인덱스와 변화하기 전의 값에 대한 정보를 스택에 저장해 두면 간단하게 되돌릴 수 있습니다.
구현체는 아래와 같습니다. Undo 연산은 $O(1)$에 동작합니다.
struct dsu {
vector<int> p, rnk;
vector<array<int, 3> > stk;
dsu() {}
dsu(int n) {
p.resize(n); rnk.resize(n);
for(int i=0; i<n; i++) p[i] = i;
}
int Find(int n) { // 정점 n이 속한 집합의 루트 반환
if (n == p[n]) return n;
return Find(p[n]);
}
void Union(int a, int b) { // a가 속한 집합과 b가 속한 집합을 병합
a = Find(a); b = Find(b);
int r = 0;
if (a != b) {
if (rnk[a] > rnk[b]) swap(a, b);
if (rnk[a] == rnk[b]) r = 1;
p[a] = b;
rnk[b] += r;
}
stk.push_back({a, b, r});
}
void Undo() { // 가장 최근에 한 Union 연산을 취소
auto [a,b,r] = stk.back();
stk.pop_back();
p[a] = a;
rnk[b] -= r;
}
};
Queue-Undo 연산
자료구조에 Queue-Undo 연산을 구현하려면 롤백 연산이 존재해야 한다는 것 말고도 추가적인 조건이 있는데, 업데이트 연산들끼리 교환법칙이 성립해야 합니다. 업데이트 연산들의 순서를 바꾸더라도 쿼리에 대한 답이 달라지지 않아야 한다는 뜻입니다.
Union 연산의 순서를 바꾸면 집합의 루트가 변할 수는 있지만, 정점들끼리의 연결성은 변하지 않습니다.
if (Find(a) == Find(b)) { ... }
여기에서는 위 코드처럼 두 정점이 같은 집합에 속하는지만을 물어볼 것이기 때문에 Union 연산 간에 교환법칙이 성립합니다.
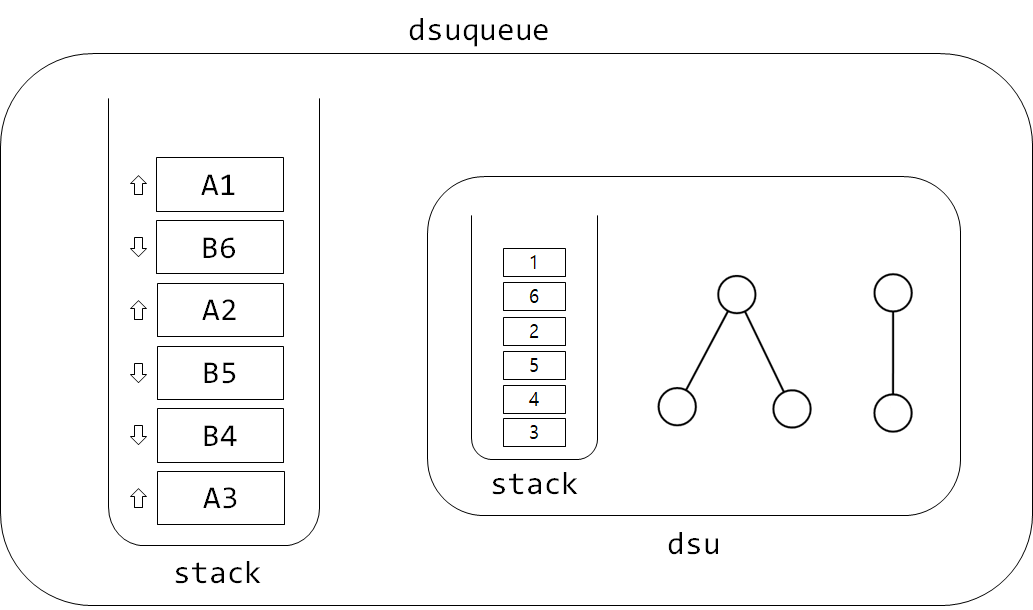
이제 dsu를 이용하는 새로운 자료구조 dsuqueue를 만들 것입니다. dsuqueue는 업데이트 연산들을 A타입과 B타입으로 분류하고 하나의 스택에 담아서 관리합니다. A타입들은 들어온 지 오래 지나서 바깥으로 빠져나가려는 연산들이고, B타입들은 들어간 지 얼마 되지 않아서 안쪽으로 들어가려는 연산들이라고 생각할 수 있습니다.
dsuqueue의 아이디어는 스택 순서를 Union 연산들이 들어온 순서대로 유지하지 않고, 쿼리 중간마다 Union 연산들의 순서를 재조정해서 오래된 업데이트들이 Undo로 나오기 쉽게 만들어 주는 것입니다.
이제 새로운 Union 연산과 Queue-Undo 연산의 동작을 살펴보겠습니다.
Union
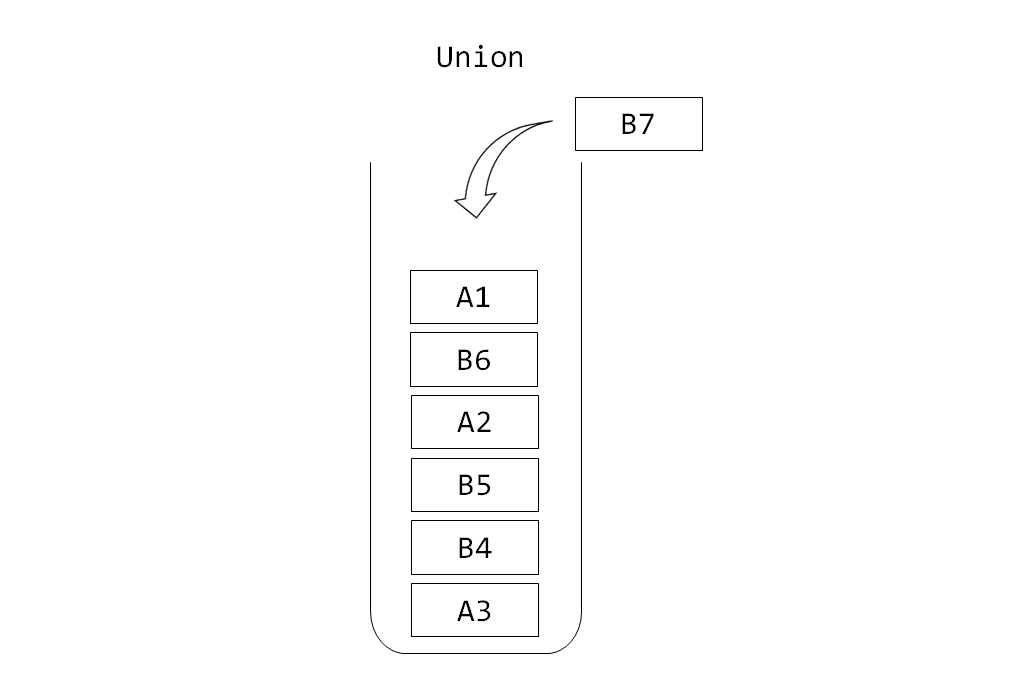
Union 연산의 동작은 간단합니다. 새로운 Union 연산이 들어오면, 이 연산을 B타입으로 분류해서 스택에 넣고 실제 dsu에서도 Union을 진행합니다.
Queue-Undo
Queue-Undo 연산이 호출되면 시간복잡도를 맞추기 위해 3가지 케이스로 분류합니다.
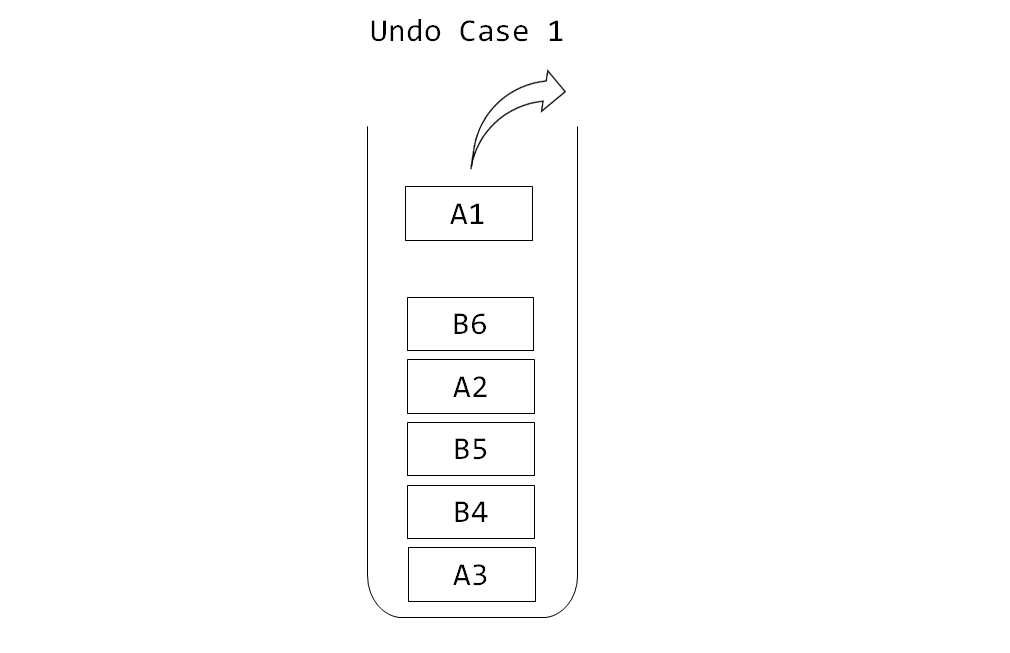
- 스택의 입구에 A타입 연산이 있을 경우, 이 연산이 가장 오래된 연산이므로 바로 빼내면 됩니다.
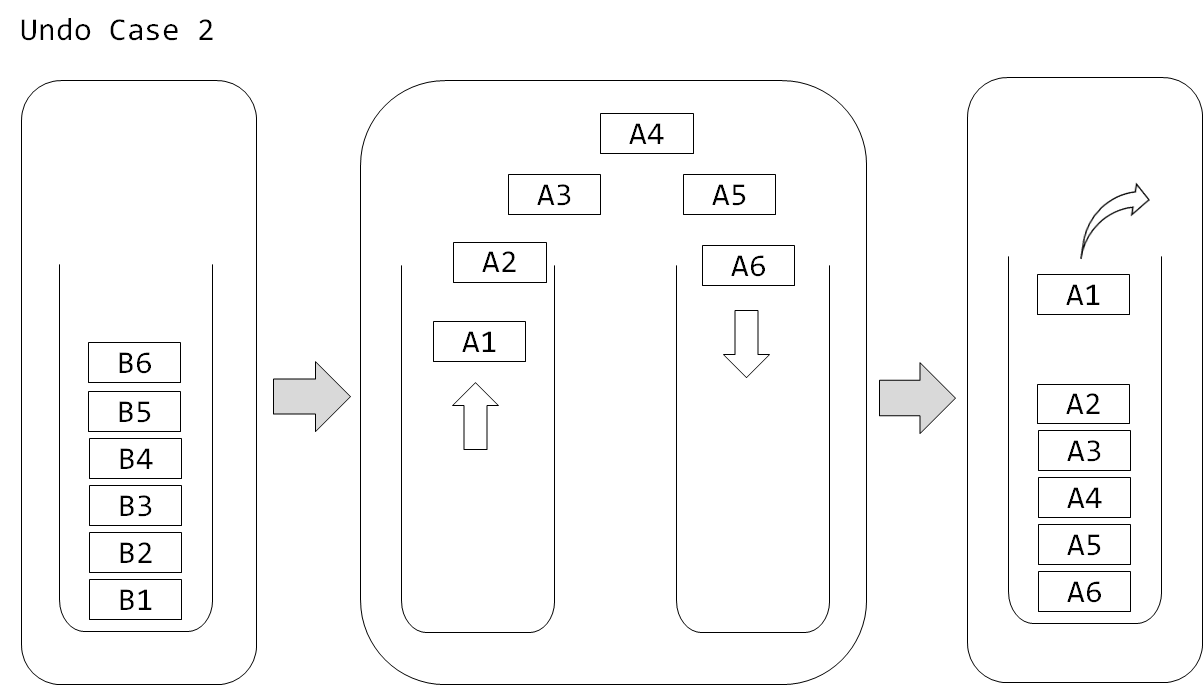
- 스택에 A타입 연산이 하나도 없고 B타입 연산만 남았을 경우, 모든 연산을 빼내고 A타입으로 바꾸어서 빼낸 순서대로 다시 삽입합니다. 이제 스택의 입구에 있는 A타입 연산을 빼내면 됩니다.
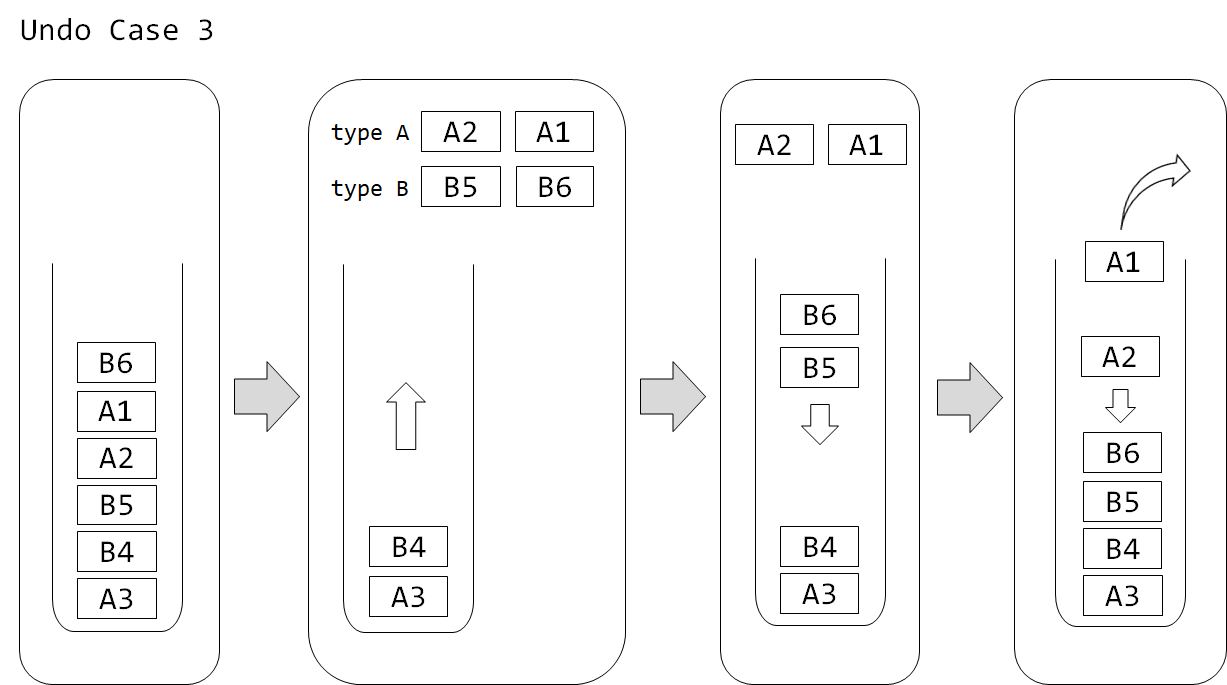
- 스택에 A타입 연산은 있지만 입구에는 B타입 연산이 있는 경우, 스택의 입구에서 연산을 하나씩 빼내는데, 빼낸 A타입 연산의 개수와 B타입 연산의 개수가 같아지거나 A타입 연산을 모두 빼낼 때까지 계속합니다. 이후 B타입 연산들을 빼낸 역순으로 삽입한 뒤, A타입 연산들을 빼낸 역순으로 삽입합니다. 이제 스택의 입구에 있는 A타입 연산을 빼내면 됩니다.
시간복잡도
업데이트 연산이 $Q$회 일어나면 dsu에는 Union 연산과 Undo 연산이 Amortized $O(Q\log{Q})$번 호출되고, 최종 시간복잡도는 Amortized $O(Q\log{Q}\log{N})$이 됩니다.
위처럼 복잡한 과정을 수행하면 왜 시간복잡도가 보장되는지 직관적으로 알기 어렵지만, 이에 대한 증명을 모르더라도 뒤에서 다룰 문제들을 해결하는 데에는 지장이 없으므로 생략하겠습니다. Queue-Undo의 아이디어를 처음으로 소개한 원본 글에 자세한 증명이 나와 있으니, 궁금하신 분들은 읽어 보시기 바랍니다.
구현
구현체는 아래와 같습니다. A타입 연산은 숫자 0, B타입 연산은 숫자 1로 나타내겠습니다.
struct dsuqueue {
dsu uf;
int z; // A타입 연산의 개수
vector<array<int, 3> > stk; // {연산의 타입, a, b}
dsuqueue(int n) {
uf = dsu(n);
z = 0;
}
int Find(int n) {
return uf.Find(n);
}
void Union(int a, int b) {
uf.Union(a, b);
stk.push_back({1, a, b});
}
void Undo() {
if (z == 0) { // case 2: A타입 연산이 없는 경우
for(int i=0; i<stk.size(); i++)
uf.Undo();
reverse(stk.begin(), stk.end());
for(auto &it : stk)
uf.Union(it[1], it[2]), it[0] = 0;
z = stk.size();
}
if (stk.back()[0] == 1) { // case 3: 입구에 B타입 연산이 있는 경우
vector<array<int, 3> > v[2];
while(v[0].empty() || v[1].empty() || (z != v[0].size() && v[0].size() != v[1].size())) {
v[stk.back()[0]].push_back(stk.back());
stk.pop_back();
uf.Undo();
}
for(int i : {1, 0})
while(!v[i].empty()) {
stk.push_back(v[i].back());
v[i].pop_back();
uf.Union(stk.back()[1], stk.back()[2]);
}
}
// case 1: 입구에 A타입 연산이 있는 경우
uf.Undo();
z--;
stk.pop_back();
}
};
연습 문제
BOI 2020 Day 1. Joker
문제 요약: 정점 $N$개, 간선 $M$개인 무향 그래프와 쿼리 $Q$개가 주어집니다. $i$번 쿼리마다 $[l_{i},r_{i}]$구간의 간선을 제거한다면 홀수 사이클이 존재하는지를 판별해야 합니다.
간선 배열을 두 번 이어 붙이면 $l^\prime_{i}=r_{i}+1$, $r^\prime_{i}=l_{i}-1+M$일 때 $[l^\prime_{i},r^\prime_{i}]$구간의 간선만 남기는 쿼리로 바꾸어서 생각할 수 있습니다.
그래프 $G$에서의 홀수 사이클의 존재성 판별은 정점 개수가 2배인 새로운 그래프 $G^\prime$에서의 연결성 문제로 바꾸어서 생각할 수 있습니다. $G$에서 $(a,b)$간선을 추가할 때 $G^\prime$에서 $(a,\neg{b})$간선과 $(\neg{a},b)$간선을 추가하고, $G$에서 $a$가 홀수 사이클에 속하는지는 $G^\prime$에서 $a$와 $\neg{a}$가 같은 컴포넌트에 속하는지로 판별하면 됩니다.
$1 \leq r \leq 2M$에서 $L[r]$을 $[l,r]$구간의 간선들만 남겼을 때 홀수 사이클이 없는 최소의 $l$이라고 정의합시다. $L$ 배열을 전처리할 수만 있다면 각 쿼리에 대한 답을 $O(1)$에 구할 수 있습니다.
핵심 관찰(단조성): $1 \leq r \leq 2M-1$에서 $L[r] \leq L[r+1]$이 성립합니다.
dsuqueue를 이용한 투 포인터 알고리즘으로 $L$을 모두 채울 수 있고, 최종 시간복잡도는 $O(M\log{M}\log{N}+Q)$가 됩니다.
dsu와 dsuqueue를 생략한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
int N, M, Q;
pair<int, int> e[200000];
int L[400000];
int main() {
scanf("%d %d %d", &N, &M, &Q);
for(int i=0; i<M; i++) {
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
e[i] = {a, b};
}
dsuqueue graph(N+N);
for(int r=0,l=0; r<M+M; r++) { // 투 포인터
auto [a,b] = e[r%M];
graph.Union(a, b+N);
graph.Union(a+N, b);
while(graph.Find(a) == graph.Find(a+N))
graph.Undo(), graph.Undo(), l++;
L[r] = l;
}
while(Q--) {
int l, r;
scanf("%d %d", &l, &r);
l--; r--;
if (L[l-1+M] <= r+1) printf("NO\n");
else printf("YES\n");
}
return 0;
}
2020 서울대학교 프로그래밍 경시대회 Division 1. 직선형 분자 만들기
$[l,r]$ 구간의 정점들만 남긴 induced subgraph가 직선형임은 다음의 세 조건을 만족함과 같습니다.
- 모든 정점의 차수가 2 이하이다.
- 사이클이 없다.
- 간선 개수가 $r-l$이다.
1번 조건과 2번 조건을 먼저 처리하겠습니다.
$L_{1}[r]$을 $[l,r]$구간의 정점들만 남겼을 때 모든 정점의 차수가 2 이하인 최소의 $l$이라고 정의합시다.
$L_{2}[r]$을 $[l,r]$구간의 정점들만 남겼을 때 사이클이 없는 최소의 $l$이라고 정의합시다.
$1 \leq r \leq N-1$에서 $L_{1}[r] \leq L_{1}[r+1]$과 $L_{2}[r] \leq L_{2}[r+1]$이 성립하므로 두 배열 모두 투 포인터로 채울 수 있습니다. 특히 $L_{1}$은 차수 배열만 관리하면 되므로 간단합니다. 그러나 $L_{2}$는 간선의 추가/제거가 아니라 정점의 추가/제거를 요구하기 때문에 dsuqueue를 바로 가져다 쓰기 어렵습니다. 이에 대한 해결책으로, 정점을 추가할 때마다 이 정점을 한쪽 끝으로 하는 모든 간선에 대해 Union을 호출하면서, 같은 간선에 대한 Union이 두 번째로 호출될 때에만 실제 병합을 수행하도록 dsu를 수정하는 방법이 있습니다.
이제 3번 조건만이 남았습니다. $e_{r}[l]$을 $[l,r]$ 구간에 완전히 포함되는 간선의 개수라 하면, 각 $r$마다 $\max(L_{1}[r],L_{2}[r]) \leq l \leq r$과 $e_{r}[l]+l=r$을 만족하는 $l$의 개수를 구해야 합니다.
여기서 두 가지 관찰이 필요합니다.
-
$e_{r}$에서 $e_{r+1}$로 가는 상태 전이는 $r+1$번 정점에 연결된 간선 개수만큼의 구간 덧셈이다.
-
2번 조건에 의해 사이클이 없으려면 간선 개수가 $r-l$ 이하이므로, $e_{r}[l]+l \leq r$이 항상 성립한다.
투 포인터를 이동하면서, 구간 최댓값과 그 개수를 구할 수 있는 레이지 프로퍼게이션 세그먼트 트리를 관리하면 됩니다. 최종 시간복잡도는 $O(MlogMlogN)$이 됩니다.
전체 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
struct dsu {
map<pair<int, int>, int> m; // m[{a,b}] = Union(a,b)의 호출 횟수 (unordered)
vector<int> p, rnk;
vector<tuple<int,int,int,map<pair<int,int>,int>::iterator> > stk; // 정점 쌍에 대응되는 map iterator를 추가로 저장
dsu() {}
dsu(int n) {
p.resize(n); rnk.resize(n);
for(int i=0; i<n; i++) p[i] = i;
}
int Find(int n) {
if (n == p[n]) return n;
return Find(p[n]);
}
void Union(int a, int b) {
auto it = m.insert({make_pair(min(a,b),max(a,b)),0}).first;
int r = 0;
if (++it->second == 2) { // 두 번째 Union일 때에만 실제로 병합
a = Find(a); b = Find(b);
if (a != b) {
if (rnk[a] > rnk[b]) swap(a, b);
if (rnk[a] == rnk[b]) r = 1;
p[a] = b;
rnk[b] += r;
}
}
stk.push_back({a, b, r, it});
}
void Undo() {
auto [a,b,r,it] = stk.back();
stk.pop_back();
if (--it->second == 1) // 두 번째 Union이었을 경우에만 실제로 취소
p[a] = a, rnk[b] -= r;
}
};
struct dsuqueue {
dsu uf;
int z; // A타입 연산의 개수
vector<array<int, 3> > stk; // {연산의 타입, a, b}
dsuqueue(int n) {
uf = dsu(n);
z = 0;
}
int Find(int n) {
return uf.Find(n);
}
void Union(int a, int b) {
uf.Union(a, b);
stk.push_back({1, a, b});
}
void Undo() {
if (z == 0) { // case 2: A타입 연산이 없는 경우
for(int i=0; i<stk.size(); i++)
uf.Undo();
reverse(stk.begin(), stk.end());
for(auto &it : stk)
uf.Union(it[1], it[2]), it[0] = 0;
z = stk.size();
}
if (stk.back()[0] == 1) { // case 3: 입구에 B타입 연산이 있는 경우
vector<array<int, 3> > v[2];
while(v[0].empty() || v[1].empty() || (z != v[0].size() && v[0].size() != v[1].size())) {
v[stk.back()[0]].push_back(stk.back());
stk.pop_back();
uf.Undo();
}
for(int i : {1, 0})
while(!v[i].empty()) {
stk.push_back(v[i].back());
v[i].pop_back();
uf.Union(stk.back()[1], stk.back()[2]);
}
}
// case 1: 입구에 A타입 연산이 있는 경우
uf.Undo();
z--;
stk.pop_back();
}
};
int N, M;
vector<int> g[250001], edges[250001];
int deg[250001], lazy[530000];
struct Node {
int mx, cnt;
Node() { mx = 0, cnt = 1; }
bool operator<(const Node &n) const {
return mx < n.mx;
}
} seg[530000];
void Propagate(int n, int l, int r) {
if (lazy[n]) {
if (l != r) {
lazy[n*2] += lazy[n];
lazy[n*2+1] += lazy[n];
}
seg[n].mx += lazy[n];
lazy[n] = 0;
}
}
void Update(int L, int R, int val, int n=1, int l=1, int r=250000) { // [L,R] 구간에 val 덧셈
Propagate(n, l, r);
if (r < L || R < l) return;
if (L <= l && r <= R) {
lazy[n] += val;
Propagate(n, l, r);
return;
}
int mid = (l+r)/2;
Update(L, R, val, n*2, l, mid);
Update(L, R, val, n*2+1, mid+1, r);
seg[n] = max(seg[n*2], seg[n*2+1]);
if (seg[n*2].mx == seg[n*2+1].mx)
seg[n].cnt = seg[n*2].cnt + seg[n*2+1].cnt;
}
int main()
{
scanf("%d %d", &N, &M);
for(int i=0; i<M; i++) {
int a, b;
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
long long res = 0;
dsuqueue graph(N+1);
for(int r=1,l=1; r<=N; r++) { // 투 포인터 한 번으로 1,2,3번 조건을 동시에 관리
Update(r, r, r);
for(int x : g[r]) {
while(l <= x && x < r && (deg[x] == 2 || deg[r] == 2 || graph.Find(x) == graph.Find(r))) {
// 1번 조건: l과 연결된 모든 정점의 차수 감소
for(int y : edges[l])
deg[y]--;
deg[l] = 0;
// 2번 조건: l을 한쪽 끝으로 하는 모든 간선 Queue-Undo
for(int i=0; i<g[l].size(); i++)
graph.Undo();
// 3번 조건: l은 앞으로 답에서 제외
Update(l, l, -1234567890);
l++; // l 삭제
}
graph.Union(x, r); // 2번 조건: r을 한쪽 끝으로 하는 모든 간선 Union
if (l <= x && x < r) {
// 1번 조건: r과 연결된 모든 정점의 차수 증가
deg[x]++;
deg[r]++;
edges[x].push_back(r);
// 3번 조건: 간선 개수 관리
Update(1, x, 1);
}
}
if (seg[1].mx == r)
res += seg[1].cnt;
}
printf("%lld\n", res);
return 0;
}
Bubble Cup 13 Finals. Virus
dsu에서 size 배열만 추가하면 풀리는 기초 문제입니다.
Codeforces Round #681. Sum
핵심 관찰을 하고 나면, 새로운 물건을 추가하거나 가장 오래된 물건을 제거하며 0-1 배낭 문제의 답을 구하는 문제로 변형할 수 있습니다.
이제 knapsack DP에 Queue-Undo 연산을 구현하면 $O(knlogn)$에 해결할 수 있습니다.