Centroid of a Tree
Centroid는 트리에서 문제를 해결하는 경우에 중요한 역할을 하는 경우가 많습니다. 이번 글에서는 트리에서 정의되는 centroid가 무엇인지, 어떤 성질을 가지고 있는지 그리고 어떻게 사용하는지 등을 알아보고자 합니다.
Centroid
트리에서 centroid는, 어떤 정점 $v$가 크기 $n$짜리 트리 $T$에서 삭제했을 경우 생기는 subtree들이 모두 각각 크기가 $n/2$ 이하가 되는 경우, $v$를 $T$의 centroid라고 합니다.

위 그림에서는 1번 노드가 centroid 입니다. 1을 삭제했을 때 각각 크기가 3, 4, 4인 서브트리가 생기고 전체 트리의 크기는 11이므로 위에 말한 조건을 만족하기 때문입니다.
그렇다면 centroid는 어떤 트리에서 존재할까요?
Theorem 1.1. 임의의 트리 $T$에는 항상 centroid가 하나 이상 존재한다
Proof. 크기 $n$짜리 트리 $T$면 다음과 같은 알고리즘을 생각해 봅시다.
- T에서 임의의 정점 $v$를 고른다.
- $v$를 삭제했을때 생기는 subtree들이 모두 $n/2$ 이하이면 $v$가 centroid이므로 알고리즘을 마친다.
- 아닌경우 $n/2$ 보다 큰 서브트리 하나가 존재할 것이다. (두 개 이상 존재하면 $T$의 크기가 $n$이라는 조건에 모순 발생) 그 서브트리의 루트를 $u$라고 할때, $v$를 $u$로 바꿔주고 2. 로 돌아간다.
이때, 같은 정점은 다시 방문되지 않을 것입니다. 그 이유는, 만약 $v$에서 $u$로 이동했다는 것은, $u$의 크기가 $n/2$ 보다 크다는 것이고, $u$ 기준에서 $v$를 루트로 하는 서브트리는 $n/2$이하일 것이기 때문에 이 알고리즘에서 $v$를 다시 방문할 일은 없을 것이기 때문입니다.
따라서 정점의 개수는 $n$으로 정해져 있기 때문에, $n$번 이하의 반복으로 $T$에서 centroid를 항상 찾을 수 있을 것입니다.
Theorem 1.1 증명과 동시에 임의의 트리에서 centroid를 찾는 알고리즘을 알게 되었습니다. 이것을 직접 코드로 구현해보면 다음과 같습니다.
vector<int> G[MAXN]; // 그래프의 인접리스트
int S[MAXN]; // S[x]: x를 루트로 하는 서브트리의 크기
// init(cur, par): S 배열의 값을 계산해주는 함수
int init(int cur, int par) {
S[cur] = 1;
for(int nxt : G[cur]) if(nxt != par) {
S[cur] += init(nxt, cur);
}
return S[cur];
}
// centroid(cur, par, sz): init 후 트리의 centroid를 반환하는 함수
int centroid(int cur, int par, int sz) {
for(int nxt : G[cur]) if(nxt != par) {
if(sz / 2 < S[nxt]) {
return centroid(nxt, cur, sz);
}
}
return cur;
}
이제 centroid는 항상 존재하다는 것은 확인했습니다. 그렇다면 centroid는 최대 몇 개까지 존재할 수 있을까요?
Theroem 1.2. 임의의 트리 $T$에서 centroid는 최대 2개 까지 존재할 수 있다.
Proof. 크기 $n$짜리 임의의 트리 $T$에서 centroid가 3개 이상 존재한다고 가정해 봅시다. 첫 번째 centroid를 $x$라고 했을때, $x$를 기준으로 한 subtree들이 모두 $n/2$보다 작으면 $x$를 제외한 모든 존점은 $x$를 포함하는 서브트리가 $n/2$보다 클 것이므로 centroid가 될 수 없고 이는 가정에 모순입니다. 따라서 정확히 $n/2$인 subtree는 항상 하나 존재할 것입니다. 그 subtree의 루트를 y라고 합시다. 이때, $y$를 기준으로 x를 루트로하는 서브트리는 크기가 $n/2$일 것이고, 나머지 subtree는 $n/2$ 보다 작을 것입니다. 따라서 $y$는 두 번째 centroid 입니다. 하지만, 방금 언급한 것 처럼 나머지 subtree는 $n/2$ 보다 작을 것이므로, 그 subtree들에서는 위에 말한 이유에서 centroid인 정점이 존재할 수 없습니다. 따라서 $x$와 $y$가 유일한 centroid가 될 수 밖에 없고 이는 가정에 모순이므로, Theorem 1.2가 증명됩니다.
Theorem 1.2를 증명하면서 우리는 자동적으로 한 가지 사실을 알게 되었습니다. 바로 centroid가 2개 존재한다면 그 centroid들은 서로 하나의 간선으로 이어져 있다는 사실입니다.
Tip 1. Centroid가 2개인 경우 그 2개는 서로 엣지로 이어져 있습니다. 만약 centroid를 이용하는 문제에서 centroid가 2개 나오게 된다면, 그 둘을 잇는 간선에 edge division을 하여 새로운 트리를 만든다면 centroid가 새로 생긴 정점 하나로 정해지기 때문에, 관련 문제를 코드로 해결하는 경우에 가끔씩 편리한 코딩에 도움이 됩니다.
지금 까지는 centroid와 centroid를 구하는 방법, 그리고 centroid의 몇 가지 특징들을 알아 보았습니다. 다음은 centroid를 이용해서 트리 관련 문제를 해결할 때 사용할 수 있는 유명한 방법들에 대해서 알아보겠습니다.
Centroid Decomposition
알고리즘 문제들에 익숙하다면, 어떠한 수열에서 분할정복을 하는 문제를 자주 보았을 것입니다. 대표적으로 정렬 알고리즘인 Merge Sort 알고리즘이 수열에서 분할정복을 이용합니다.
수열에서 분할정복은 일반적으로 다음과 같은 단계로 이루어집니다.
- 수열의 중간 지점 $m$을 기준으로 수열을 왼쪽 오른쪽 두 개의 구간으로 나눈다.
- 왼쪽 구간과 오른쪽 구간에 대하여 부분 문제를 해결한다.
- 두 구간에서 구한 결과를 바탕으로 전체 문제를 해결한다.
Merge Sort의 경우 중간 지점 $m$을 기준으로 왼쪽 구간 오른쪽 구간에 대해서 정렬하고 그것을 바탕으로 전체 구간을 합치는 과정을 재귀 적으로 반복하여 $O(NlogN)$ 이라는 빠른 시간복잡도 안에 정렬을 완료합니다.
트리에서도 수열처럼 분할정복을 하고 싶으면 어떡할까요? 먼저 1.에 해당하는 과정을 봅시다. 수열에서는 중간 지점 $m$ 을 단순히 현재 해결하고 있는 구간 $[l, r]$에 대하여 $m = (l + r) / 2$와 같이 구할 수 있습니다. 트리에서는 어떨까요? 맞습니다. 바로 centroid를 중간 지점으로 잡는 것입니다. 이렇게 하면 수열에서 구간을 반으로 나누는 효과와 비슷한 효과를 낼 수 있기 때문입니다.
나머지도 거의 비슷합니다. 2.에 해당하는 과정의 경우 왼쪽 구간, 오른쪽 구간 대신, centroid를 기준으로 나뉘어진 subtree들에 대해서 문제를 해결 하고, 3.에 해당하는 과정은 subtree들의 결과를 바탕으로 원래 트리에서의 문제를 해결하면 됩니다.
Tip 2. 수열을 일직선인 트리(또는 chain)이라고 생각하면 수열에서 분할정복 하는 것과 트리에서 분할정복하는 것은 원리가 같다는 것을 이해하는데 편합니다.
이 과정의 기본적인 구조를 코드로 나타내면 다음과 같습니다.
vector<int> G[MAXN]; // 그래프의 인접리스트
int S[MAXN]; // S[x]: x를 루트로 하는 서브트리의 크기
int del[MAXN]; // del[x]: 이미 한번 decompse에서 centroid로 지목된 경우 1, 아니면 0
// init(cur, par): S 배열의 값을 계산해주는 함수
int init(int cur, int par) {
S[cur] = 1;
for(int nxt : G[cur]) if(nxt != par && !del[nxt]) {
S[cur] += init(nxt, cur);
}
return S[cur];
}
// centroid(cur, par, sz): init 후 트리의 centroid를 반환하는 함수
int centroid(int cur, int par, int sz) {
for(int nxt : G[cur]) if(nxt != par && !del[nxt]) {
if(sz / 2 < S[nxt]) {
return centroid(nxt, cur, sz);
}
}
return cur;
}
// decompose(root): root를 루트로하는 subtree에서 분할정복을 통해 subtree의 문제를 해결하는 함수
void decompose(int root) {
int sz = init(root, -1); // root를 기준으로하는 새로운 트리이기 때문에 새로 init
int cen = centroid(root, -1, sz); // 현재 트리에서 centroid
del[cen] = 1; // 다시 방문하지 않을 것이기 때문에 표시
// do something
for(int nxt : G[cen]) if(!del[nxt]) {
decompose(i); // cen을 기준으로하는 서브트리들에서 문제 해결
// do something
}
// do something
}
Centroid Tree
Centroid tree는 centroid decomposition 과정을 트리로써 표현한 것입니다. 이렇게 하는 이유는 한번의 분할정복 과정에서 문제를 해결하는 것이 아니라 쿼리를 받아 트리를 업데이트하는 등의 상황에서 유용하게 사용할 수 있습니다.
Centroid tree의 구조는 다음과 같습니다. 먼저 루트는 최초 트리에서의 centroid입니다. 그리고 centroid decomposition 과정을 거치면서 임의의 시점에 지목되는 centorid를 $v$라고 하고 그 시점에서 $v$를 포함하고 있는 트리를 $T$라고 합시다. Centroid tree 상에선 $v$의 자녀는 $T$에서 $v$를 제거했을때 생기는 subtree 들의 centroid들 입니다.
말로써는 이해가 안갈 수 있으니 다음 애니메이션으로 이해해봅시다.
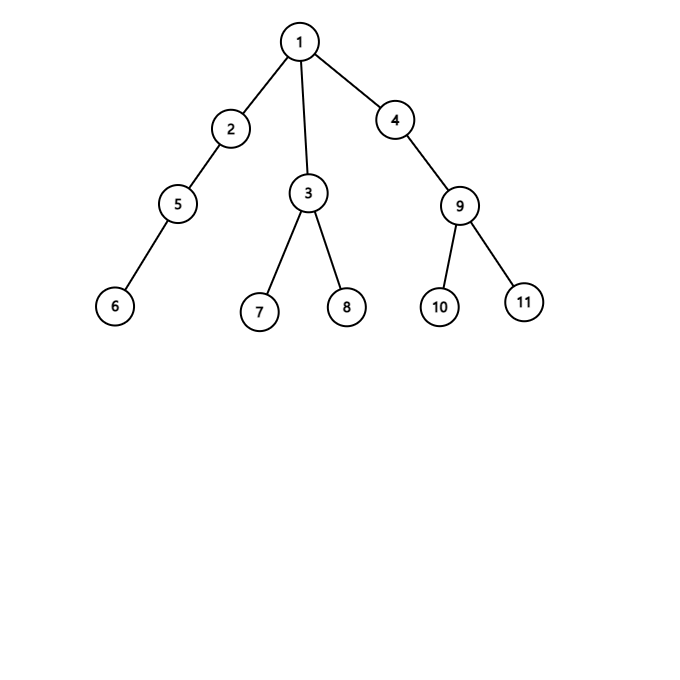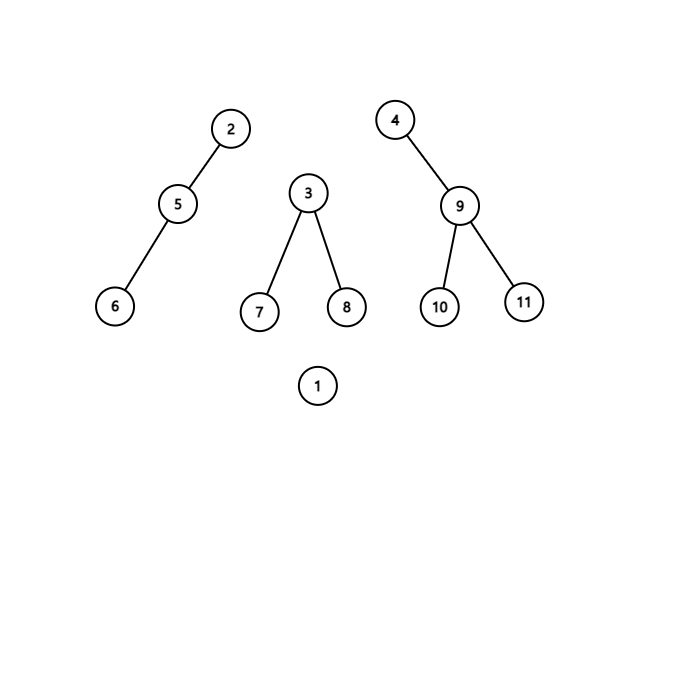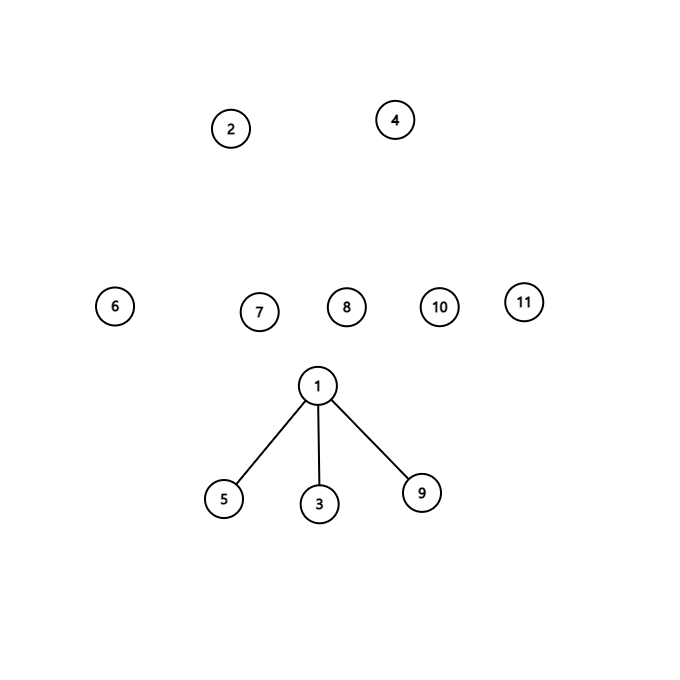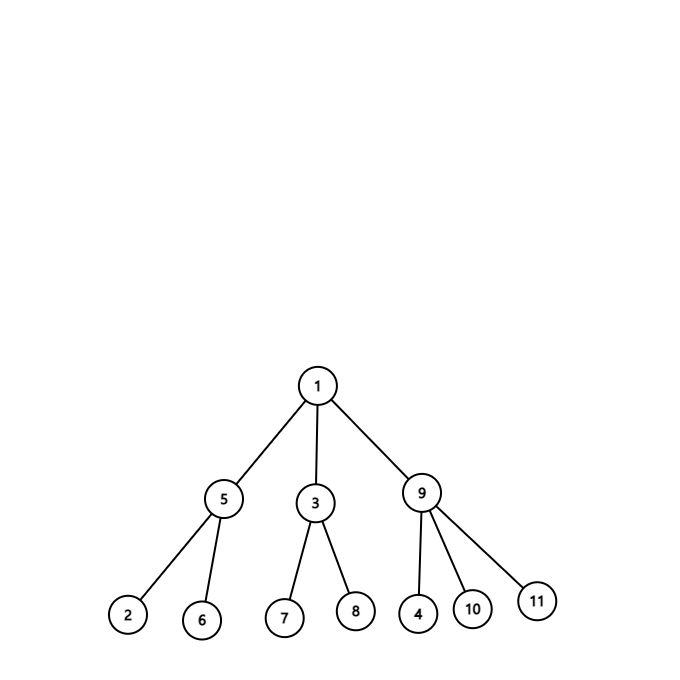
처음에 centroid는 1이므로 centroid tree의 루트는 1이 될 것입니다. 그 다음 생긴 subtree 3개에서 centroid는 가각 5, 3, 9 임을 알 수 있습니다. 따라서 centroid tree 상에서 1의 자녀들은 5, 3, 9가 될 것입니다. 마지막으로, 5의 자녀들은 5를 제거했을때 남은 서브트리의 centroid인 2, 6이고, 3의 자녀들은 7, 8, 그리고 9의 자녀들은 4, 10, 11이 됩니다.
이 centroid tree는 몇 가지 유용한 성질들이 있습니다.
Theorem 3.1. 크기 $N$ 짜리 트리 $T$의 centroid tree의 높이는 $log_{2}N$ 이하이다.
Proof. 귀납법으로 증명할 수 있습니다.
- 먼저 $N = 1, 2, 3$ 인 경우에는 직접 확인 가능합니다.
- $k > 2$인 $k$에 대하여 $k$ 이하인 모든 $N$에서 성립한다고 가정합시다. 이때, $N = 2k$인 트리에서 centroid를 삭제했을때 남는 subtree들은 모두 크기가 $k$ 이하일 것이므로, subtree들이 각각 만드는 centroid tree들의 높이들 중 최댓값은 가정 때문에 $log_{2}k$ 이하일 것입니다. 따라서 크기가 $N = 2k$인 centroid tree의 높이의 최댓값은 $log_{2}k + 1 = log_{2}2k$ 이므로 $N = 2k$ 일때도 성립합니다.
- $N = 2k +1$ 일때 비슷한 이유로 성립합니다.
- 따라서 모든 $N$에 대해서 Theorem 3.1이 성립함을 알 수 있습니다.
Theorem 3.2. 트리 $T$의 임의의 두 정점 $x, y$를 선택했을때, centroid tree 상에서 $x, y$의 least commmon ancestor를 $l$ 이라고 하면, $T$상에서 $x$와 $y$사이 경로에는 $l$이 포함된다.
Proof. Centroid decomposition을 진행할 때, $x$와 $y$가 같은 트리에서 속해있다가 서로 다른 트리 $T_{1}$과 $T_{2}$로 갈라지는 시점에서 centroid를 $v$라고 합시다. 그럼 $x$와 $y$ 모두 $v$ 기준에서의 subtree에 속하기 때문에 $v$가 common ancestor임을 알 수 있습니다. 이후에, $x$의 경우는 나머지 조상들은 모두 $T_{1}$에 있는 정점들 중 하나로 결정될 것입니다. 마찬가지로 $y$의 경우 나머지 조상들은 모두 $T_{2}$에 있는 정점들 중 하나로 결정될 것입니다. 하지만 $T_{1} \cap T_{2} = \phi$ 이므로 더 이상 $x$와 $y$의 common ancestor은 나오지 않습니다. 따라서 $v$가 $x$와 $y$의 least common ancestor가 됩니다. 이때 $T$상에서 $x$와 $y$모두 $v$ 기준에서 서로 다른 subtree에 속했기 때문에 $T$상에서 $x$와 $y$를 잇는 경로는 무조건 $v$를 지나갈 것 입니다. 따라서 증명이 완료됩니다.
Tip 3. Theorem 3.2에 의해서 임의의 정점 $v$에서 시작하는 모든 경로는 $v$또는 $v$의 centroid tree 상의 조상들을 중 하나를 지난다는 것을 알 수 있습니다. 또한 Theorem 3.1에 의해서 $v$의 조상의 개수는 $log_{2}N$ 이하입니다. 따라서 이것을 잘 이용한다면 어려워 보이는 쿼리들을 빠른 시간안에 처리할 수 있는 경우가 자주 있습니다.
Tip 3.에서 언급한 것 처럼 위 정리들을 잘 기억하고 있으면 트리 상에서 문제를 해결할 때 강력한 도구로써 centroid tree를 사용할 수 있습니다. 좀 더 감을 잡고 싶으시면, 아래에 centroid decompostion, centroid tree들을 이용하는 연습문제들 몇 개를 올려두었으니 연습해보시기 바랍니다.
마지막으로 centroid tree의 기본 구조를 구현한 코드로 설명을 마무리하겠습니다.
vector<int> G[MAXN]; // 그래프의 인접리스트
int S[MAXN]; // S[x]: x를 루트로 하는 서브트리의 크기
int del[MAXN]; // del[x]: 이미 한번 decompse에서 centroid로 지목된 경우 1, 아니면 0
int P[MAXN]: // P[x]: centroid 트리 상에서 x의 부모
// init(cur, par): S 배열의 값을 계산해주는 함수
int init(int cur, int par) {
S[cur] = 1;
for(int nxt : G[cur]) if(nxt != par && !del[nxt]) {
S[cur] += init(nxt, cur);
}
return S[cur];
}
// centroid(cur, par, sz): init 후 트리의 centroid를 반환하는 함수
int centroid(int cur, int par, int sz) {
for(int nxt : G[cur]) if(nxt != par && !del[nxt]) {
if(sz / 2 < S[nxt]) {
return centroid(nxt, cur, sz);
}
}
return cur;
}
// decompose(root, bef): root를 루트로하는 subtree에서 분할정복을 통해 subtree의 문제를 해결하는 함수
void decompose(int root, int bef) {
int sz = init(root, -1); // root를 기준으로하는 새로운 트리이기 때문에 새로 init
int cen = centroid(root, -1, sz); // 현재 트리에서 centroid
del[cen] = 1; // 다시 방문하지 않을 것이기 때문에 표시
P[cen] = bef; // bef 자녀에 cen 추가
// do something
for(int nxt : G[cen]) if(!del[nxt]) {
decompose(i, cen); // cen을 기준으로하는 서브트리들에서 문제 해결
// do something
}
// do something
}
Centroid를 활용하는 연습문제 리스트
- https://codeforces.com/contest/161/problem/D
- https://codeforces.com/contest/321/problem/C
- https://codeforces.com/contest/766/problem/E
- https://www.acmicpc.net/problem/5820
- https://www.acmicpc.net/problem/13514