Stack 자료구조와 실습

Stack

Stack이란

스택 자료구조란 항상 한쪽 방향에서만 자료의 입력 및 출력이 가능한 형태의 선형 자료구조입니다. 책상 위에 책을 무더기로 쌓아놓은 상태를 생각하면 스택 구조를 이해하기 쉽습니다. 여러 개의 책이 쌓인 상태에서, 우리는 가장 위에 놓여져 있는 책만 쉽게 들어올릴 수 있으며, 가장 위에만 새롭게 책을 놓는 것이 쉽습니다. 물론 중간에 있는 위치에 책을 넣거나 빼는 것도 가능하지만, 이를 위해서는 그보다 위에 있는 책들을 들어야 하죠. 여기서 가장 위에 있는 책이라는 의미는, 책들이 쌓이기 시작했을 때 가장 마지막에 쌓인 책이라는 뜻이 됩니다.

스택도 마찬가지로 선형구조에서, 존재하는 자료들 중 가장 마지막에 들어온 자료만을 접근하거나, 혹은 그 위치 바로 뒤에 자료를 추가하는 것이 가능합니다. 이처럼 마지막 위치에서 입,출력이 일어나는 구조를 LIFO(Last-In-First-Out) 라고 부릅니다. 마지막으로 들어온 자료가 처음으로 나가게 되며, 처음으로 들어온 자료가 나머지 모든 자료가 나간 후에야 마지막으로 나가게 되기 때문입니다.

구현

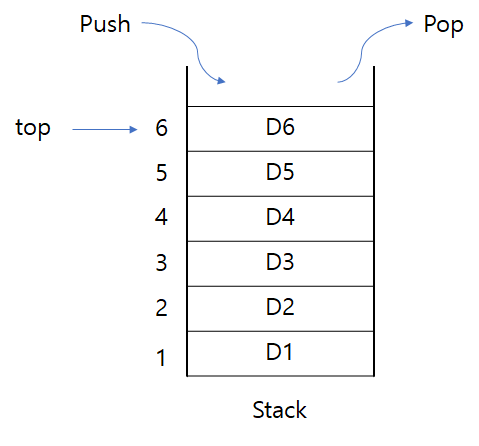
Stack 자료구조

스택 자료구조에서 가장 중요한 역할을 하는 것은 바로 ‘top’ 입니다. top은 스택 내 가장 마지막 원소를 가리키고 있으며, stack의 거의 모든 연산은 top을 이용해서 해결하는 것이 가능합니다.

스택에서 지원하는 연산들은 다음과 같습니다.

Stack.top() = 스택 내 가장 마지막에 들어온 원소를 반환합니다. top이 가리키는 원소를 반환합니다.
Stack.push(a) = 스택의 마지막 위치 뒤에 새로운 a 자료를 추가합니다. 이 경우, top이 가리키는 위치가 1단계 증가하게 됩니다.
Stack.pop() - 스택의 가장 마지막 위치에 있는 원소를 제거합니다. top이 가리키는 원소를 제거한 후, top의 위치가 1단계 감소하게 됩니다.
Stack.size() - 스택 내 원소의 수를 반환합니다. 구현에 따라 다르나, 스택 내 첫 원소의 위치를 1이라 했을 때, top이 가리키고 있는 단계가 size가 됩니다.
Stack.empty() - 스택이 비어있는지 여부를 반환합니다. top이 0단계를 가리키고 있을 경우 참을, 그렇지 않을 경우 거짓을 반환합니다.

이외에도 다른 연산들을 추가할 수 있으며, 이는 스택을 구현할 때 사용하는 자료구조에 따라서도 달라질 수 있습니다.

스택을 구현하는 자료구조는 크게 2가지가 있습니다.

배열
연결 리스트

배열을 사용해서 구현할 경우, 임의 접근(random access)이 가능해집니다. 우리가 top의 위치를 가지고 연산을 하는 것 뿐만 아니라, 스택 내부에 있는 원소들도 배열의 인덱싱을 통한 접근이 가능해집니다. 이 경우 삽입과 삭제를 구현하기 보다는, 중간에 있는 값을 확인하여 사용하거나 값을 변경하는데에 의의가 조금 더 큽니다.

허나 스택을 사용해야하는 경우에는, 중간에 있는 값을 접근하는 것에 큰 의미가 없는 경우가 많습니다. 그러한 이유로, 연결 리스트를 이용해서 스택을 구현하는 것과 큰 차이가 없게 됩니다.

사용하는 경우

재귀함수

스택 자료구조 자체를 처음 들어보더라도, 이미 스택의 아이디어를 사용하여 동작하고 있는 것 중 우리가 알고 있는 내용이 있습니다.

바로 함수에서 또 다른 함수를 호출하는 경우들이 그러하며, 그 중 가장 유명한 것으로 자기자신을 호출하는 ‘재귀함수’가 있습니다. (C언어를 기준으로 설명하겠습니다)

A함수에서 B함수를 호출했다고 합니다. 이 경우, 우리는 A 함수를 동작하고 있다가도, B함수를 호출하는 부분에서 멈춘 후, B함수를 동작하게 됩니다. 이 과정에서, 현재까지 동작한 A함수의 상태를 저장하고 있지 않다면, B함수를 동작한 이후 다시 A함수로 돌아와도, 어떤 부분에서부터 코드 동작을 이어나갈지에 대한 정보를 알 수가 업습니다.

이를 해결하기 위해서, 함수는 자신이 호출 될 때에 그 함수의 상태를 스택을 통해서 관리해줍니다.

A함수가 호출될 때에 스택에 A함수의 현재 상태를 저장하면서 진행해 나갑니다. 그러다가 B함수가 호출될 경우, 스택에 A함수의 현재 상태까지 저장해놓은 후 중단하고, B함수의 시작 상태를 스택에 새롭게 추가하게 됩니다. 이 경우, 항상 현재 동작하는 부분은 스택에 가장 마지막에 들어온 함수가 동작합니다. 이후 B함수의 동작이 모두 끝나게 되면 스택에서 B함수를 제거하게 되고, 다시 스택의 가장 마지막 자료를 확인하게 됩니다. 이 때, 스택에는 A함수가 남아있으며, 중단한 위치는 B함수를 호출하는 구문에서 중단되었다는 정보를 스택 자료를 통해 알아 낼 수 있게 됩니다. 이를 사용하여 A함수를 다시 동작할 때, 처음부터 동작하는 것이 아닌 B함수를 호출한 이후의 위치부터 동작하는 것이 가능해집니다.

이와 같은 구조는 함수를 호출할 때마다 함수 상태를 스택에 저장하는 것으로 구현됩니다.

이 때문에 발생하는 문제 중, 한 번씩 겪어보았을 문제가 있습니다.

stackoverflow on function call

바로 함수를 관리하는 스택이 초과하여 overflow가 나는 경우입니다. 함수를 관리하는 Stack도 결국 메모리를 사용하기 때문에, 최대치 이상의 함수 호출이 스택을 통해 관리된다면 메모리가 부족하게 되어 stackoverflow가 발생하게 됩니다. 보통 C언어의 경우 몇십만 회 이상의 함수 호출이 쌓여있는 경우 발생하게 되며, 이는 설정을 통해 function call에 메모리를 추가로 할당하거나, 혹은 재귀함수를 자신이 직접 stack을 통해 구현하여 해결하는 방법 등이 있습니다.

알고리즘 문제 해결

스택을 알고리즘 문제 해결에서 사용하는 경우, 굉장히 많은 스택의 사용법은 다음 조건을 만족시키기 위해 사용됩니다.

스택 내부가 특별한 정렬 순서로 유지되어야 할 경우

스택을 사용하는 문제 중 위 조건을 만족해야하는 문제의 경우, 실제 문제를 해결하는 과정을 보면서 설명하도록 하겠습니다.

스택을 사용하는 문제 1

KOI 2019 막대기

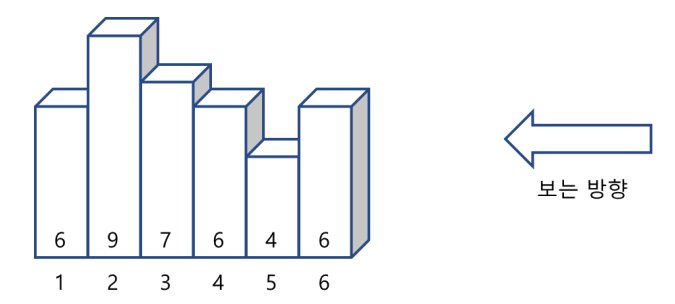
막대기 (출처:한국정보올림피아드 2019 1차 대회 문제)

위 문제를 읽고 오신 후, 충분히 생각해보신 다음, 아래 내용들을 읽어보시길 바랍니다. 문제의 풀이는 단계적으로 해결해나가는 과정을 적어나갔으며, 그 사이에 스택을 사용하게 되는 이유와 적용시키는 방법을 서술하였습니다.

관찰

주어진 N개의 막대가 오른쪽에서 보았을 때, 보이기 위한 특별한 조건은 무엇일까요? 어떤 막대가 보인다는 것은, 그 막대의 오른쪽에 있는 막대기들 중 자신보다 더 큰 막대는 존재하지 않는다는 것으로 해석할 수 있습니다.

즉, 우리는 모든 막대들에서부터 오른쪽으로 살펴보아, 자신보다 큰 막대가 있는지 살펴볼 수 있습니다. 또한 만약에 자신과 높이가 같은 막대가 존재해도, 자신이 보이지 않고 그보다 오른쪽에 더 가까운 같은 높이의 막대에 의해 가려지기 때문에, 자신의 높이 이상의 막대가 존재하는지를 살펴보는 방식을 이용해야합니다.

이를 통해, 우리는 각각 N개의 막대마다 오른쪽에 있는 막대를 살펴보는 방법으로 각 막대의 보이는 여부를 O(N)에 찾아줄 수 있습니다.

이를 모든 막대에 수행하게 되므로, 우리는 총 O(N^2)에 문제를 해결할 수 있습니다.

풀이

막대의 개수가 더 많아질 경우에, N^2은 문제를 해결하기에 충분히 빠르지 않을 수 있습니다. 그러므로 우리는 더 좋은 방법으로 문제를 해결할 수 있는지 살펴볼 필요가 있습니다.

우리에게 가장 문제가 되는 부분은, 오른쪽으로 가면서, 자신보다 크거나 같은 막대기가 있는지를 확인하는 과정이 너무 오래 걸린다는 것입니다. 이를 해결하기 위해서 우리는 다음의 두 가지 접근을 해볼 수 있습니다.

오른쪽에 자신보다 큰 막대기의 존재 여부를 빠르게 찾아주거나
다른 방향으로 접근해보기

이 중, 우리는 다른 방향으로 접근해보는 것을 생각해봅시다. 어떤 방법으로 위 문제를 다르게 해석해볼 수 있을까요?

우리는 이것을 다음과 같이 접근해볼 수도 있습니다.

순서대로 보면서, 자신보다 왼쪽에 있는 막대 중 자신보다 작거나 같아서 보이지 않는 막대를 제거하는 방법

아까의 우리는 오른쪽에서 자신을 가리는 막대를 살펴보는 방법으로 접근했습니다. 이번에는 어떤 막대가 자신의 왼쪽의 막대를 가리는 경우를 제거하여, 남아서 보이는 막대가 몇 개 있는지 세는 방법을 사용해봅시다. 앞선 본문의 예시를 사용해봅시다.

첫 막대의 경우, 자신보다 왼쪽에 있는 막대가 없으므로 일단 보일 수 있다 둘 수 있습니다. 두 번째 막대의 경우 자신의 왼쪽에 6을 가리므로, 6은 보이지 않는다는 것을 알 수 있습니다. 세 번째 막대의 경우, 자신의 왼쪽에 있는 6을 가린다는 것을 알 수 있습니다. 허나 이미 6은 9에 의해 가려진다는 정보를 아까 두 번째 단계에서 확인할 수 있었습니다. 우리는 이러한 ‘이미 불가능한 막대’를 다시 확인하는 일을 없애서 중복으로 세는 경우를 없애고 싶습니다. 어떤 방법을 이용할 수 있을까요?

우리는 앞서 배운 ‘스택(stack)’ 자료구조를 생각해볼 수 있습니다. 스택을 이용하여 앞선 예시를 살펴보겠습니다.

다음과 같은 막대들이 주어지고 우리에게 빈 스택이 있다 생각해봅시다. 또한 스택에서 관리가 되는 막대들을 ‘현재 단계에서, 오른쪽에서 보았을 때 보이는 막대’ 들이라 합시다.

매 단계에 추가되는 막대의 경우, 항상 오른쪽에서 가장 가까운 막대이므로 항상 보인다는 것을 알 수 있어, 첫 막대 6은 보인다는 것을 알 수 있습니다.

두 번째 막대의 경우, 높이가 9인 막대입니다. 이 때, 스택 내부에서 가장 위에 있는 막대를 봅시다. 이 때의 막대의 경우 높이가 9보다 작기 때문에 보일 수 없게 되어 스택에서 제거됩니다. 이후, 스택에는 9만 남아있게 됩니다.

세 번째 막대의 경우 높이가 7인 막대입니다. 스택 내 마지막 막대의 경우 7보다 크므로, 오른쪽에서 봐도 보인다는 것을 알 수 있습니다.

네 번째 막대인 6의 경우, 스택 내 마지막 막대인 7보다 작아서 7이 남아있게 된다는 것을 알 수 있습니다. 그렇다면 스택의 마지막 원소 외의 막대는 어떻게 될까요?

사실, 스택 내 원소들은 항상 ‘내림차순’ 이 유지될 수 밖에 없습니다. 만약 어떤 원소가 그 다음 원소보다 더 값이 작거나 같았다면, 해당 원소를 확인할 때에, 자신보다 크기가 작거나 같으므로 항상 스택 내에서 제거가 되었을 것이기 때문입니다. 즉, 다른 원소들은 모두 7보다 큰 상태이므로, 우리는 추가로 확인하지 않고 6을 스택 내에 추가시키면 됩니다.

다섯 번째 막대인 4의 경우도, 스택 내 마지막 원소인 6이 더 크므로, 스택에 추가됩니다.

여섯 번째 막대인 6을 볼 때, 스택 내 마지막 원소인 4가 더 작으므로, 4를 스택에서 제거합니다.

이후, 스택 내 마지막 원소인 6 또한 6보다 작거나 같으므로 스택에서 제거되어야합니다.

스택 내 마지막 원소는 6보다 크므로, 6을 스택에 추가하는 것으로 마치게 됩니다.

결국 우리는 마지막 단계에서 스택 내에 3개의 원소가 들어있으므로, 답이 3이 됨을 알 수 있습니다.

그렇다면, 스택을 이용했을 때의 시간복잡도는 어떻게 될까요?

우리는 모든 막대를 확인할 때마다, 각 막대는 한 번씩만 스택에 추가되고 제거된다는 사실을 알 수 있습니다. 즉 우리는 N개의 막대를 약 2번 씩만 확인하게 되므로, 총 O(N)의 시간복잡도로 문제를 해결할 수 있습니다.

스택 내부가 특별한 정렬 순서로 유지되어야 할 경우

이 과정에서, 스택 내부는 항상 내림차순으로 유지된다는 것을 알 수 있습니다. 새롭게 오른쪽에서 나오는 막대기의 경우, 자신이 왼쪽으로 볼 때에 만나게 되는 자신보다 작거나 같은 막대기들을 지우는 과정이 필요하기 때문에, 항상 모든 막대를 기준으로 자신의 왼쪽에는 큰 막대만 남아있게 되어, 결국 내림차순이라는 결과가 나오게 됩니다.

문제를 해결하는 과정에서, 정렬 순서를 유지하기 위해서 스택 사용 <=> 스택을 사용하여 조건을 만족하다 보니 정렬 순서 이 둘 중 어떤 것이 먼저인지는 문제에 적용하려는 접근방법에 따라 달라지겠지만, 결과적으로 우리가 이야기한 경우에 해당한다는 것을 알 수 있습니다.

번외 풀이

우리는 이를 해결하는 방향을 바꾸는 것으로도 쉽게 해결할 수 있습니다.

주어진 막대기 6 9 7 6 4 6 을 다시 봅시다.

오른쪽의 6의 경우, 자신이 가장 오른쪽에 있으므로 항상 보일 수 밖에 없습니다. 이후, 4의 경우, 6보다 작으므로 보일 수 없고, 6도 마찬가지로 보일 수 없습니다. 7의 경우, 6보다 크므로 보인다는 것을 알 수 있고, 다음으로 나오는 9 또한 7보다 크므로 보인다는 것을 알 수 있습니다. 이후 6의 경우, 지금까지 나온 값 중 최댓값인 9보다 작으므로 보일 수 없어서 답은 3이 됩니다.

이렇게 매 번 현재까지 나온 막대 중 최대높이를 기억하여, 보일 수 있는지 여부를 바로 판단하여 O(N)에 해결할 수 있습니다.

스택을 사용하는 문제 2

KOI 2015 지역본선 쇠막대기

쇠막대기 (출처:한국정보올림피아드 2015 지역본선)

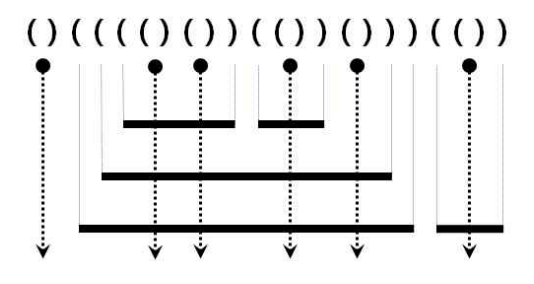
스택을 사용하는 문제 중 괄호를 사용하는 문제를 빼놓고 이야기하는 어렵습니다. 위 문제도 함께 해결해봅시다.

관찰

주어진 괄호 안에서 레이저는 무조건 ()와 같이 바로 옆에 짝이 맞춰진 상태로 주어지게 됩니다. 즉, 이렇지 않고, 바로 옆에 짝이 맞지 않은 괄호들은 무조건 막대기에 속한다는 것을 알 수 있습니다.

그렇다면, 막대기의 수는 어떻게 알 수 있을까요? 주어지는 문자열은 모두 괄호의 짝이 맞기 때문에, 레이저와 막대기의 수의 합은 항상 전체 문자열 길이의 절반이 됩니다. 즉, 우리는 (전체 문자열 길이 / 2) - (레이저의 수) 만큼의 막대기가 존재한다는 것을 알 수 있습니다. 이제 필요한 일은, 각각의 막대기가 몇 개의 조각으로 부서지는지 세기만 하면 됩니다.

만약 하나의 막대기 사이에 3개의 레이저가 있다면, 그 막대기는 총 4개의 조각으로 나뉘게 됩니다. 마찬가지로 k개의 레이저가 한 막대기 위에 있다면, 그 막대기는 k+1개의 조각으로 나뉘게 됩니다.

우리는 앞선 정보를 통해, 막대기 사이에 있는 () 문자열의 수를 세는 것으로 답을 어렵지 않게 구할 수 있습니다.

길이 n의 문자열에는 총 n/2개의 열린 괄호가 있습니다. 앞에서부터 차례대로 하나의 열린 괄호가 총 몇 조각으로 나뉘는지 구해봅시다. 하나의 열린 괄호에 대해, 이와 짝이 되는 닫힌 괄호는 이전 문제 ‘괄호’에서 스택을 이용해 해결해보았습니다. 다시 한 번, 스택을 이용해 문제를 해결해보겠습니다.

’(‘만 존재할 경우, 이는 현재 막대기보다 짧은 막대기이므로, ‘)’도 먼저 발견하게 됩니다. ‘괄호’에서처럼 스택에 넣은 후, ‘)’를 발견하면 빼줍니다.
’()’의 경우 레이저이므로, 발견한 레이저의 수를 증가시켜줍니다.
스택에 하나의 ‘(‘만 존재하고, 현재 ‘)’를 발견했다면, 우리가 보고있는 막대기의 끝에 도달한 것이므로 종료합니다.

이처럼 각 막대에 해당하는 레이저의 수를 구해주면, 잘려진 조각의 총 수를 쉽게 구할 수 있습니다. 우리가 보는 막대기의 수는 최대 n/2, 스택을 이용해 찾는 과정에서 최대 n번 보게 되므로, O(n^2)에 문제를 해결할 수 있습니다.

풀이

위의 O(N^2) 풀이로도 어느정도 크기의 데이터들을 처리할 수 있습니다만, 우리는 더 빠르게 문제를 해결하고 싶습니다. 이 때, 우리는 관찰에서 얻은 정보들과, 낭비하는 시간을 최적화 하여 활용하고 싶습니다.

각 막대기의 조각 수는 (해당하는 레이저의 수) + 1 이었으므로, 구하고자 하는 답은 (각 막대기에 해당하는 레이저 수의 합) + (막대기의 수) 가 됩니다.
‘스택’ 과정에서 위에 쌓이는 막대기는 무시하고 지나갔습니다. 이번에는 위에 쌓이는 막대기의 정보 또한 이용해봅시다.

위 두 개를 이용해 좀 더 빠르게 문제를 해결하고 싶습니다. 아까는 ‘하나의 막대기가 몇 조각으로 나뉘는지’를 세었다면, 이번에는 ‘각 레이저가 몇 개의 막대기를 지나는지’를 세어 해결해봅시다.

먼저, ‘괄호”에서 진행한 것처럼, 막대기에 해당하는 ‘(‘의 경우 스택에 넣어줍니다. 그리고 이후에 ‘()’에 해당하는 레이저가 등장할 경우, 우리는 현재 스택에 있는 열린 괄호의 수가 곧 레이저가 지나는 막대기의 수임을 어렵지 않게 알 수 있습니다. 스택에 남아있지 않다면, 아직 막대기의 시작이 나오지 않았거나, 이미 끝났을 것이기 때문입니다.

즉, 우리는 ‘()’의 발견 때마다 스택에 들어있는 원소의 수를 세주고, 이 과정에서 스택에 들어간 열린 괄호의 수를 세주면, 이 둘의 합이 곧 (레이저가 관통한 막대기의 수) + (막대기의 수)가 되어, 답이 됨을 알 수 있습니다.

이 때에, 우리는 각 문자를 최대 한 번만 보게 되고, 각 문자는 스택에 최대 한 번 들어가고 빠지기 때문에, 많아야 한 문자에 대해 3번을 넘게 보지 않습니다.

결국 총 시간 복잡도는 O(N)이되어 위 방법보다 더 빠르게 해결할 수 있게 됩니다.

‘스택 내부가 특별한 정렬 순서로 유지되어야 할 경우’ 와의 관계

쇠막대기 문제에서 괄호를 사용하여 스택을 구현하는 것이, 도대체 왜 스택 내부가 정렬 순서로 유지되는 것과 연관이 있는지 궁금할 수 있습니다. 물론 이 문제를 해결할 때에는 위에 언급된 내용이 문제풀이를 위해 필수적으로 고려해야하는 점은 아닙니다.

하지만 실제로 스택 내부를 살펴보면, 열린 괄호가 관리되는 것이 특별한 정렬 순서를 유지하고 있다는 것을 알 수 있습니다.

스택에서 제거되는 열린 괄호는 항상 가장 마지막으로 들어온 괄호가 됩니다. 닫힌 괄호가 등장할 때에, 항상 자신에게 가장 가까운 열린 괄호가 매치되는 괄호이기 때문에, 결국 나중에 등장한 괄호가 먼저 나가게 되므로 스택 자료구조를 사용하게 됩니다.

이 때, 괄호들을 그저 괄호 자체로 보는 것이 아닌, 괄호가 등장하는 순서(index)를 기준으로 생각해봅시다.

스택 내부에서 열린 괄호들은 항상 괄호가 등장하는 순서가 오름차순으로 된다는 것을 알 수 있습니다.

하지만 이 문제에서, 스택 내부의 괄호는 오름차순이 유지되었지만, 오름차순으로 유지된다는 성질 자체는 문제를 해결하기 위해 사용되지는 않습니다. 왜냐하면 우리가 현재 보고 있는 괄호의 경우, 앞에 나와있던 괄호들이 자신보다 ‘먼저’ 나왔다는 정보가 중요할 뿐이지, ‘얼마나 먼저’에 대한 여부는 중요하지 않기 때문입니다.

즉, 우리는 앞서 나온 열린 괄호 라는 점만 중요할 뿐이지, 이들이 유지되는 순서는 중요하지 않게 됩니다. 즉, 순서를 유지할 필요가 없게 되므로, 열린 괄호들을 스택을 통해 관리해줄 필요가 없이, 현재까지 열려있는 괄호의 개수 만을 관리해주는 것으로 스택을 사용하는 것과 같은 효과를 낼 수 있게 됩니다.

이외에도 다양한 문제들을 스택을 사용할 때 유지되는 성질을 통해서 해결할 수 있습니다.

이후의 스택 포스팅을 통해서는 스택의 성질을 사용하여 해결할 수 있는 문제들을 정리해보겠습니다.

코드

막대기_스택

#include <bits/stdc++.h>
using namespace std;

int n;
stack <int> st;

int main(){
  int i, a;
  scanf("%d", &n);
  for(i = 0; i < n; i++){
    scanf("%d", &a);
    while(!st.empty() && st.top() <= a) st.pop();
    st.push(a);
  }
  printf("%d", st.size());
  return 0;
}

막대기_번외풀이

#include <bits/stdc++.h>
using namespace std;

int n, res, max1;
int arr[100010];

int main(){
	int i;
	scanf("%d", &n);
	for(i = 0; i < n; i++) scanf("%d", &arr[i]);
	for(i = n - 1; i >= 0; i--) if(arr[i] > max1) max1 = arr[i], res++;
	printf("%d", res);
	return 0;
}

쇠막대기_열린 괄호의 수만 유지

#include <bits/stdc++.h>
using namespace std;

int res,cnt,n;
char arr[100010];

int main(){
    int i;
    scanf("%s",arr);
    n=strlen(arr);
    for(i=0;i<n-1;i++){
        if(arr[i]!=arr[i+1] && arr[i]=='('){
            res+=cnt; i++;
        }
        else if(arr[i]=='(')cnt++;
        else{
            res++; cnt--;
        }
    }res+=cnt;
    printf("%d",res);
}