Integer Partition
개요
고등학교 교육과정의 확률과 통계 과목에서도 볼 수 있었던 자연수의 분할은 DP로 계산할 수 있어서 PS에서도 종종 등장하는 주제입니다. 이 글에서는 자연수 분할의 점화식과 빠르게 계산하는 방법, 그리고 문제풀이에서의 활용을 다룹니다.
자연수 $n$을 자연수 $k$개의 합으로 나타내는 방법의 수를 $P(n,k)$라고 합시다.
자연수 $n$을 분할하는 방법의 수를 $P(n)=\sum_{k=1}^{n}P(n,k)$이라 합시다.
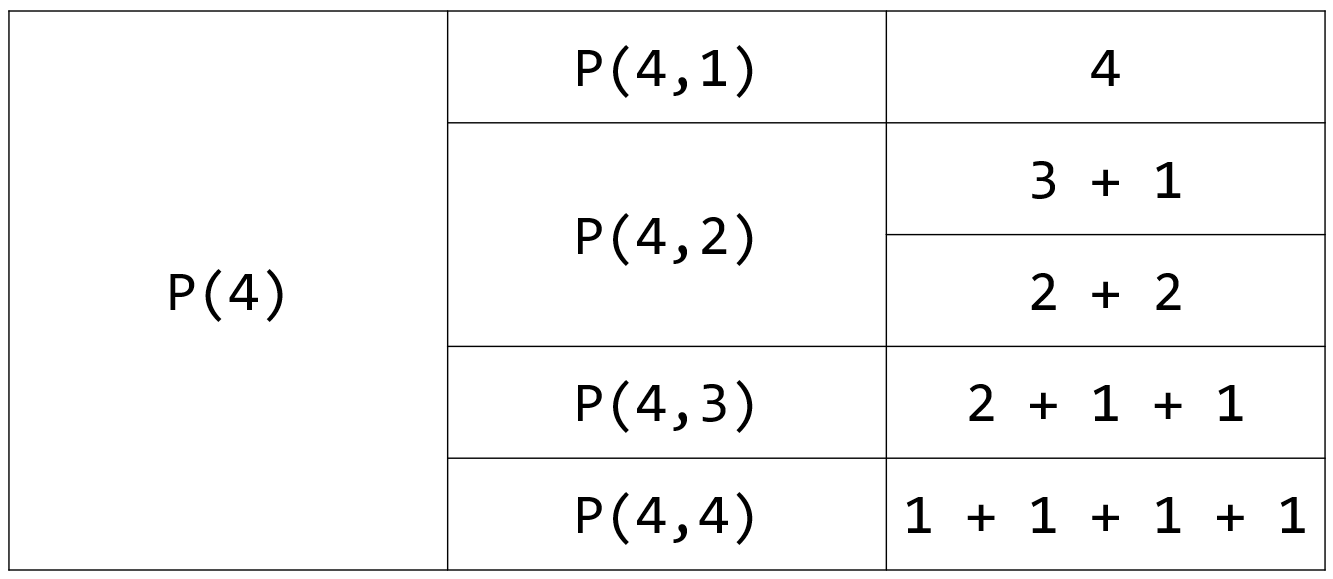
예를 들어, 4를 분할하는 방법의 수는 위 그림처럼 5가지가 됩니다.
$P(n,k)$를 $O(nk)$에 계산하는 방법
$P(n,k)$를 직접 구하는 간단한 공식은 알려져 있지 않고, 보통 점화식을 통해 계산합니다.
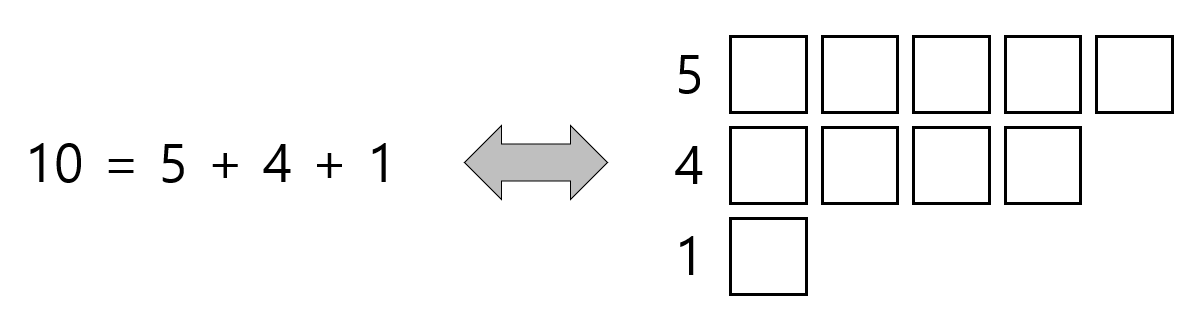
위 그림처럼, $P(n,k)$의 각 방법은 행이 $k$개, 사각형이 $n$개이고 아래로 내려갈수록 행의 길이가 단조감소하는 그림과 일대일 대응시킬 수 있습니다. 이러한 그림을 Young diagram(또는 Ferrers diagram)이라 부릅니다.

Young diagram을 통해 시각적으로 보면 $P(n,k)$의 방법들은 두 가지 케이스로 나눌 수 있습니다.
- 마지막 행의 길이가 1인 방법의 수는 $P(n-1,k-1)$
- 마지막 행의 길이가 2 이상인 방법의 수는 $P(n-k,k)$
따라서 다이나믹 프로그래밍으로 $O(nk)$에 계산할 수 있습니다.
이 방법으로 $P(n)$을 구하려면 $O(n^2)$의 시간이 걸리지만, 아래에서는 $P(n)$의 계산에 특화된 효율적인 방법들을 소개합니다.
$P(n)$을 $O(n \sqrt{n})$에 계산하는 방법 (1)
분할수의 생성함수에 오일러의 오각수 정리(pentagonal number theorem)를 적용하면 $P(n)$을 $O(n \sqrt{n})$에 구할 수 있습니다. OEIS에 의하면, 점화식은 다음과 같습니다.
$P(n)=\sum_{j=1}^{\left\lfloor\frac{1+\sqrt{1+24n}}{6}\right\rfloor}(-1)^{j-1}P(n-\frac{j(3j-1)}{2})+\sum_{j=1}^{\left\lfloor\frac{-1+\sqrt{1+24n}}{6}\right\rfloor}(-1)^{j-1}P(n-\frac{j(3j+1)}{2})$
코드는 다음과 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define MOD 998244353
int P[500001];
int main() {
P[0] = 1;
for(int i=1; i<=500000; i++) {
for(int j=1; j*(3*j-1)/2<=i; j++)
P[i] += (j%2?1:-1)*P[i-j*(3*j-1)/2], P[i] %= MOD;
for(int j=1; j*(3*j+1)/2<=i; j++)
P[i] += (j%2?1:-1)*P[i-j*(3*j+1)/2], P[i] %= MOD;
P[i] += MOD, P[i] %= MOD;
}
return 0;
}
$P(n)$을 $O(n \sqrt{n})$에 계산하는 방법 (2)
오일러의 오각수 정리를 이용한 방법이 코딩하기에는 편하지만, 이해하기 까다롭고 점화식을 변형해서 활용하기 어렵다는 단점이 있습니다. 이어서 소개할 방법은 더 직관적이고, 어려운 사전지식이 필요 없으며, 역시 $O(n \sqrt{n})$에 작동합니다.
$N$이 주어졌을 때 $P(1),\cdots,P(N)$을 모두 $O(N \sqrt{N})$에 구할 것입니다. $N=9$를 예시로 들겠습니다.

위 그림에서 격자 바깥에 있는 모든 칸은 값이 0이므로 고려하지 않아도 됩니다.
먼저, 처음에 구한 $P(n,k)=P(n-1,k-1)+P(n-k,k)$ 점화식을 이용해 $1 \leq n \leq N, 1 \leq k < \lfloor \sqrt{N} \rfloor$인 $P(n,k)$들을 전처리합니다. 그림에서 회색 칸들이 이에 해당하고, $O(N \sqrt{N})$의 시간이 걸립니다.
예시로, 파란색 칸을 보면 $P(9,4)=P(8,3)+P(5,4)$인 상태 전이를 확인할 수 있습니다.
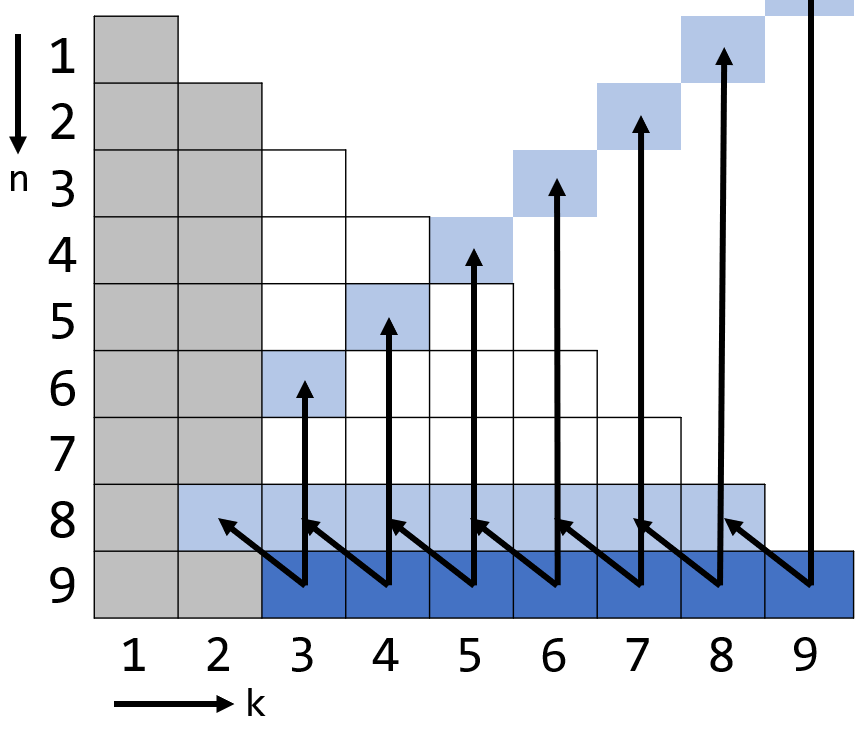
$P(n)$은 $n$번째 행에 놓인 모든 칸의 합이므로, 한 행을 통째로 상태 전이할 경우 어떻게 변화하는지 관찰해 봅시다. 파란색 칸들을 보면 직선에서 직선으로의 상태 전이이므로, 직선에 대한 점화식을 세울 수 있습니다.
$D(a,b)$를 기울기가 $-a$이고 점 $(\lfloor\sqrt{N}\rfloor, b)$에서 출발하는 반직선, 다시 말해 $n=-a(k-\lfloor\sqrt{N}\rfloor)+b$와 $k \geq \lfloor \sqrt{N} \rfloor$를 만족하는 $(n,k)$칸들의 합이라고 정의합시다.
$P(n)=\left(\sum_{k=1}^{\lfloor\sqrt{N}\rfloor-1} P(n,k)\right) + D(0,n)$이므로, $D(0,n)$들만 구하면 $O(N \sqrt{N})$시간에 모든 $P(n)$도 구할 수 있습니다.
파란색 칸들을 보면 점화식 $D(a,b)=D(a,b-a-1)+D(a+1,b-\lfloor\sqrt{N}\rfloor)+P(b-1,\lfloor\sqrt{N}\rfloor-1)$이 성립합니다. $a$가 $1$만큼 증가할 때마다 $b$는 적어도 $\lfloor\sqrt{N}\rfloor$만큼 감소하므로, $0 \leq a \leq \lfloor\sqrt{N}\rfloor$과 $\lfloor\sqrt{N}\rfloor \leq b \leq N$을 만족하는 $D(a,b)$만 계산하면 되고 최종 시간복잡도는 $O(N \sqrt{N})$이 됩니다.
마지막으로 공간 복잡도가 문제인데, $P(n,k)$는 $k$에 대해 토글링을 하고 $D(a,b)$는 $a$에 대해 토글링을 하면 선형 메모리로 구현할 수 있습니다.
코드는 다음과 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define MOD 998244353
const int N = 500000, SQRT_N = 707;
int P[2][500001], D[2][500001], res[500001];
int main() {
res[0] = 1;
// P[k][n] 계산
for(int k=1; k<SQRT_N; k++) {
P[0][0] = (k == 1);
for(int n=1; n<=N; n++) {
int &ret = P[k&1][n];
ret = P[k-1&1][n-1];
if (n-k >= 0) ret += P[k&1][n-k], ret %= MOD;
res[n] += ret, res[n] %= MOD;
}
}
// D[a][b] 계산
for(int a=SQRT_N; a>=0; a--)
for(int b=SQRT_N; b<=N; b++) {
int &ret = D[a&1][b];
ret = 0;
if (b-a-1 >= 0) ret += D[a&1][b-a-1];
ret += D[a+1&1][b-SQRT_N], ret %= MOD;
ret += P[SQRT_N-1&1][b-1], ret %= MOD;
if (a == 0) res[b] += ret, res[b] %= MOD;
}
// res[n]이 P(n)과 같다.
return 0;
}
연습 문제
Library-Checker. Partition Function
$P(n)$을 제대로 계산하는지 테스트할 수 있는 문제입니다.
CS Academy Round #32 G. Sum of Powers
문제
$N,K,M$이 주어지면, $a_1+\cdots+a_k=N$을 만족하는 모든 multiset $\lbrace a_1, \cdots, a_K \rbrace$에 대해 $a_1^M+\cdots+a_K^M$들의 합을 $10^9+7$로 나눈 나머지를 구해야 합니다. $(1 \leq N,M \leq 4096, 1 \leq K \leq N)$
풀이
각 $1 \leq x \leq N$에 대해 $x^M$이 답에 얼마나 기여하는지를 구합시다.
multiset에서 $x^M$들 중 첫 번째로 등장하는 원소는 총 $P(N-x,K-1)$개 존재합니다.
multiset에서 $x^M$들 중 두 번째로 등장하는 원소는 총 $P(N-2x,K-2)$개 존재합니다.
…
multiset에서 $x^M$들 중 $i$번째로 등장하는 원소는 총 $P(N-ix,K-i)$개 존재합니다.
따라서 정답은 $\sum_{x=1}^{N} x^M \sum_{i=1}^{\min(\left\lfloor N/x \right\rfloor,K)} P(N-ix,K-i)$가 됩니다.
코드
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define MOD 1000000007
int N, M, K;
int P[4100][4100];
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> N >> K >> M;
P[0][0] = 1;
for(int n=1; n<=N; n++)
for(int k=1; k<=K; k++) {
P[n][k] = P[n-1][k-1];
if (n-k >= 0) P[n][k] += P[n-k][k], P[n][k] %= MOD;
}
ll res = 0;
for(int x=1; x<=N; x++) {
ll a = 1;
for(int m=1; m<=M; m++)
a *= x, a %= MOD;
ll b = 0;
for(int i=1; i<=min(N/x,K); i++)
b += P[N-i*x][K-i], b %= MOD;
res += a*b, res %= MOD;
}
cout << res << "\n";
return 0;
}
Petrozavodsk Summer 2020 - Xi Lin Contest 6. Partition Number
문제
각 테스트케이스마다 자연수 $m$과 집합 $A = \lbrace a_1,\cdots,a_n \rbrace$이 주어지면, $A$에 속하지 않는 자연수만을 사용한, $m$을 분할하는 방법의 수를 $10^9+7$로 나눈 나머지를 구해야 합니다. $(1 \leq \sum{n} \leq 500, n \leq m \leq 3 \cdot 10^5)$
풀이
먼저 $P(0),\cdots,P(m)$을 $O(m \sqrt m)$에 전처리합시다.
$even(i) :=$ 집합 $A$의 서로 다른 원소를 짝수 개 더해서 $i$를 만드는 방법의 수
$odd(i) :=$ 집합 $A$의 서로 다른 원소를 홀수 개 더해서 $i$를 만드는 경우의 수
$even(i)$와 $odd(i)$들은 knapsack DP로 $O(nm)$에 채울 수 있습니다.
포함 배제의 원리에 의해 $\sum_{i=0}^{m} (even(i)-odd(i))P(m-i)$가 정답이 됩니다.
코드
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define MOD 1000000007
int T, N, M;
int P[300001], even[300001], odd[300001];
int main() {
P[0] = 1;
for(int i=1; i<=300000; i++) {
for(int j=1; j*(3*j-1)/2<=i; j++)
P[i] += (j%2?1:-1)*P[i-j*(3*j-1)/2], P[i] %= MOD;
for(int j=1; j*(3*j+1)/2<=i; j++)
P[i] += (j%2?1:-1)*P[i-j*(3*j+1)/2], P[i] %= MOD;
}
ios::sync_with_stdio(0); cin.tie(0);
cin >> T;
while(T--) {
cin >> N >> M;
memset(even, 0, sizeof(int)*(M+1));
memset(odd, 0, sizeof(int)*(M+1));
even[0] = 1;
for(int i=1; i<=N; i++) {
int x;
cin >> x;
for(int j=M; j>=x; j--) {
even[j] += odd[j-x], even[j] %= MOD;
odd[j] += even[j-x], odd[j] %= MOD;
}
}
ll res = 0;
for(int i=0; i<=M; i++) {
res += (ll)(even[i]-odd[i])*P[M-i];
res %= MOD;
}
res += MOD; res %= MOD;
cout << res << "\n";
}
return 0;
}
Petrozavodsk Summer 2017 - DPRK Contest 2. Cube Summation
문제
$10^5$개 이하의 테스트케이스가 주어집니다.
각 테스트케이스마다 $1 \leq n \leq 10^5$이 주어지면 $\sum_{k=1}^{n} k^3 \cdot P(n,k)$를 $998,244,353$으로 나눈 나머지를 구해야 합니다.
풀이
세제곱이 까다로우므로, 문제를 다른 방식으로 서술해 봅시다.
바뀐 문제: 사각형이 $n$개인 모든 Young diagram에 대해, 행의 개수를 $k$라 하면 $1 \leq a,b,c \leq k$인 3-tuple $(a,b,c)$의 개수의 합을 구해야 합니다.
위처럼 바꾸어도 같은 문제가 되는데, 순서를 구분하는 뽑기보다 순서를 구분하지 않는 뽑기가 더 계산하기 쉬우므로 다시 문제를 바꾸겠습니다.
3개의 행을 순서 있게 뽑는 방법은 순서 없이 뽑는 방법들로 쪼갤 수 있습니다.
- $(a<b<c), (a<c<b), (b<a<c), (b<c<a), (c<a<b), (c<b<a)$
- $(a=b<c), (c<a=b), (a=c<b), (b<a=c), (b=c<a), (a<b=c)$
- $(a=b=c)$
$P(n,k,t)$를, 사각형이 $n$개이고 행이 $k$개인 모든 Young diagram에 대해, 서로 다른 $t$개의 행을 순서를 구분하지 않고 뽑는 경우의 수의 합이라고 하면, 정답은 $\sum_{k=1}^{n} 6 \cdot P(n,k,3) + 6 \cdot P(n,k,2) + 1 \cdot P(n,k,1)$이 됩니다.
$P(n,k,t)=P(n-1,k-1,t)+P(n-1,k-1,t-1)+P(n-k,k,t)$
$D(a,b,t)=D(a,b-a-1,t)+D(a,b-a-1,t-1)+D(a+1,b-\lfloor\sqrt{10^5}\rfloor,t)$ $+P(b-1,\lfloor\sqrt{10^5}\rfloor-1,t)+P(b-1,\lfloor\sqrt{10^5}\rfloor-1,t-1)$
점화식의 형태가 원래의 자연수 분할과 유사하므로, $O(n \sqrt{n})$으로 줄일 때의 방법을 똑같이 적용해서 해결할 수 있습니다.
코드
#include<bits/stdc++.h>
using namespace std;
const int MOD = 998244353, N = 100000, SQRT_N = 316;
int T;
int P[2][100001][4], D[2][100001][4], res[100001][4];
int main() {
// P[k][n][t] 계산
for(int k=1; k<SQRT_N; k++) {
P[0][0][0] = (k == 1);
for(int n=1; n<=N; n++)
for(int t=0; t<=3; t++) {
int &ret = P[k&1][n][t];
ret = P[k-1&1][n-1][t];
if (t-1 >= 0) ret += P[k-1&1][n-1][t-1], ret %= MOD;
if (n-k >= 0) ret += P[k&1][n-k][t], ret %= MOD;
res[n][t] += P[k&1][n][t], res[n][t] %= MOD;
}
}
// D[a][b][t] 계산
for(int a=SQRT_N; a>=0; a--)
for(int b=SQRT_N; b<=N; b++)
for(int t=0; t<=3; t++) {
int &ret = D[a&1][b][t];
ret = 0;
if (b-a-1 >= 0) ret += D[a&1][b-a-1][t], ret %= MOD;
if (b-a-1 >= 0 && t >= 1) ret += D[a&1][b-a-1][t-1], ret %= MOD;
ret += D[a+1&1][b-SQRT_N][t], ret %= MOD;
ret += P[SQRT_N-1&1][b-1][t], ret %= MOD;
if (t >= 1) ret += P[SQRT_N-1&1][b-1][t-1], ret %= MOD;
}
// 정답 계산
for(int n=SQRT_N; n<=N; n++)
for(int t=1; t<=3; t++)
res[n][t] += D[0][n][t], res[n][t] %= MOD;
ios::sync_with_stdio(0); cin.tie(0);
cin >> T;
while(T--) {
int n;
cin >> n;
cout << (6LL*res[n][3] + 6LL*res[n][2] + res[n][1]) % MOD << "\n";
}
return 0;
}