서로 다른 수와 쿼리

개요

다음 문제를 생각해 봅시다.

길이가 $N$인 수열 $A_1, A_2, \cdots, A_N$과 쿼리 $Q$개가 주어집니다. $i$번 쿼리마다 $l_i, r_i$가 주어지면, $[l_i,r_i]$ 구간에 존재하는 서로 다른 수의 개수를 구해야 합니다. ($1 \leq N \leq 10^5, 1 \leq Q \leq 10^5, 1 \leq A_i \leq 10^6, 1 \leq l_i \leq r_i \leq N$)

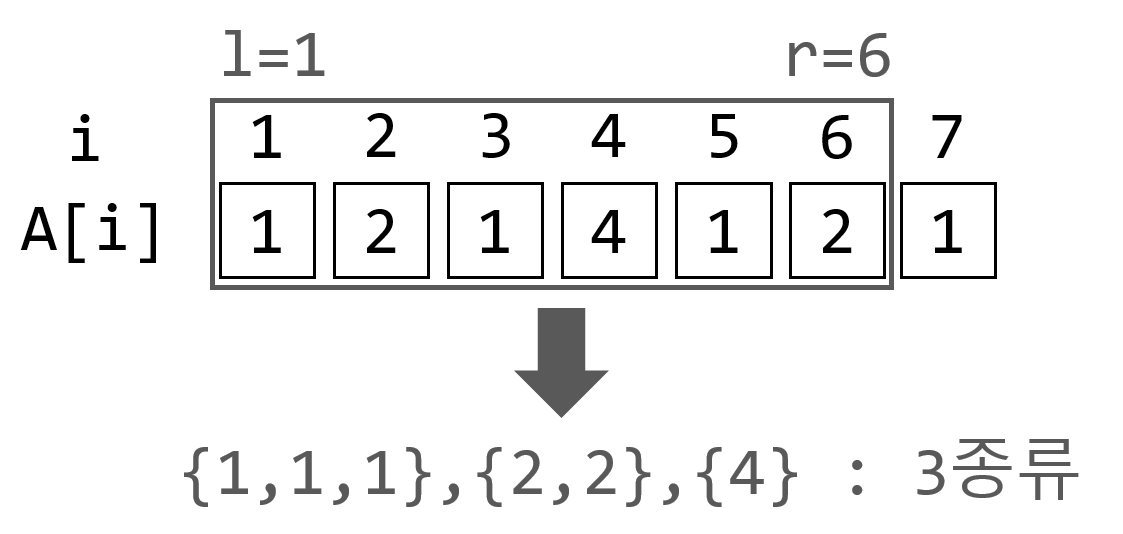
위 문제(이하 서로 다른 수와 쿼리 문제)는 problem solving을 하다 보면 가끔 맞닥뜨리게 되는데, 유명한 문제인 만큼 $O(N\sqrt{Q})$나 $O((N+Q)\log{N})$등의 다양한 풀이 방법이 존재합니다. 이 글에서는 서로 다른 수와 쿼리 문제의 몇 가지 접근 방법과 해결책, 그리고 잘 알려지지 않았지만 퍼포먼스가 뛰어난 $O((N+Q)\sqrt[3]{N})$ 풀이를 소개합니다.

오프라인 $O(N\sqrt{Q})$

만약 우리가 어떠한 $[l,r]$ 구간에 대해서,

$C[x]=$ $[l,r]$ 구간에 값 $x$가 등장하는 횟수
$cnt=$ $[l,r]$ 구간의 서로 다른 수의 개수

위와 같은 정보들을 가지고 있다면,

$[l,r] \rightarrow [l-1,r]$
$[l,r] \rightarrow [l,r+1]$
$[l,r] \rightarrow [l+1,r]$
$[l,r] \rightarrow [l,r-1]$

위 네 가지의 상태 전이를 $O(1)$에 하면서도 정보들을 관리할 수 있습니다.

$i$번 쿼리 $[l_i,r_i]$에서 $i+1$번 쿼리 $[l_{i+1},r_{i+1}]$로 이동하는 데에는 $\lvert l_i-l_{i+1} \rvert + \lvert r_i-r_{i+1} \rvert$회의 상태 전이가 필요하니, 쿼리를 차례대로 순회하며 두 포인터 $l,r$을 관리한다면 $O(QN)$의 시간복잡도로 전체 문제를 해결할 수 있습니다. 이는 너무 느린데, 개선할 방법이 있을까요?

MO’s Algorithm은 간단한 아이디어 하나를 얹어서 위 알고리즘의 시간복잡도를 $O(N\sqrt{Q})$까지 떨어트립니다. 이를 소개하는 좋은 글(링크)이 S/W멤버십 블로그에 이미 작성되어 있고, 동일한 문제가 “수열과 쿼리 5” 파트에 설명되어 있으니 읽어 보시기 바랍니다.

뒤에서 다룰 내용과 관련이 있으므로, 완전히 생략하지는 않고 간단히 소개하겠습니다.

블럭 단위로 쪼개기

적당한 블럭 크기 $B$를 고정하고, 두 쿼리 $[l_1,r_1]$, $[l_2,r_2]$에 대해 $\lfloor l_1/B \rfloor$와 $\lfloor l_2/B \rfloor$가 다르면 $\lfloor l_1/B \rfloor < \lfloor l_2/B \rfloor$인 순서대로, 같으면 $r_1 < r_2$인 순서대로 정렬합니다. 정렬한 순서대로 쿼리를 순회하며 두 포인터 $l,r$을 관리하고, 각 쿼리에 대한 답을 구합니다.

모든 쿼리를 처리하는 동안 왼쪽 포인터는 총 $O(QB+N)$칸, 오른쪽 포인터는 총 $O(\frac{N^2}{B})$칸 이동하므로 시간복잡도는 $O(QB + \frac{N^2}{B})$가 됩니다. 이 식은 산술-기하 평균 부등식에 의해 $B = \frac{N}{\sqrt{Q}}$일 때 최소화되고, 따라서 최종 시간복잡도는 $O(N\sqrt{Q})$가 됩니다.

구현

수열과 쿼리 5 문제를 해결하는 코드는 다음과 같습니다.

#include<bits/stdc++.h>
using namespace std;

const int SQ = 316;
struct MO {
	int l, r, i;
	bool operator<(const MO &n) const {
		if (l/SQ != n.l/SQ) return l < n.l;
		return r < n.r;
	}
};

int N, Q;
int A[100001], res[100001];

int cnt;
int C[1000001];

int main()
{
	ios::sync_with_stdio(0); cin.tie(0);
	cin >> N;
	for(int i=1; i<=N; i++)
		cin >> A[i];
	cin >> Q;
	vector<MO> q;
	for(int i=0; i<Q; i++)
	{
		int l, r;
		cin >> l >> r;
		q.push_back({l, r, i});
	}
	sort(q.begin(), q.end()); // 쿼리 정렬
	
	// 오프라인 쿼리
	int L = 1, R = 0;
	for(auto [l,r,i] : q)
	{
		while(l < L) if (C[A[--L]]++ == 0) cnt++; // [L,R] -> [L-1,R]
		while(R < r) if (C[A[++R]]++ == 0) cnt++; // [L,R] -> [L,R+1]
		while(L < l) if (C[A[L++]]-- == 1) cnt--; // [L,R] -> [L+1,R]
		while(r < R) if (C[A[R--]]-- == 1) cnt--; // [L,R] -> [L,R-1]
		// 이제 [L,R] == [l,r]이다.
		res[i] = cnt;
	}

	for(int i=0; i<Q; i++)
		cout << res[i] << "\n";
	return 0;
}

오프라인 $O((N+Q)\log{N})$

이번에는 다른 방식으로 접근해 봅시다.

2차원 구간 합 문제로의 변환

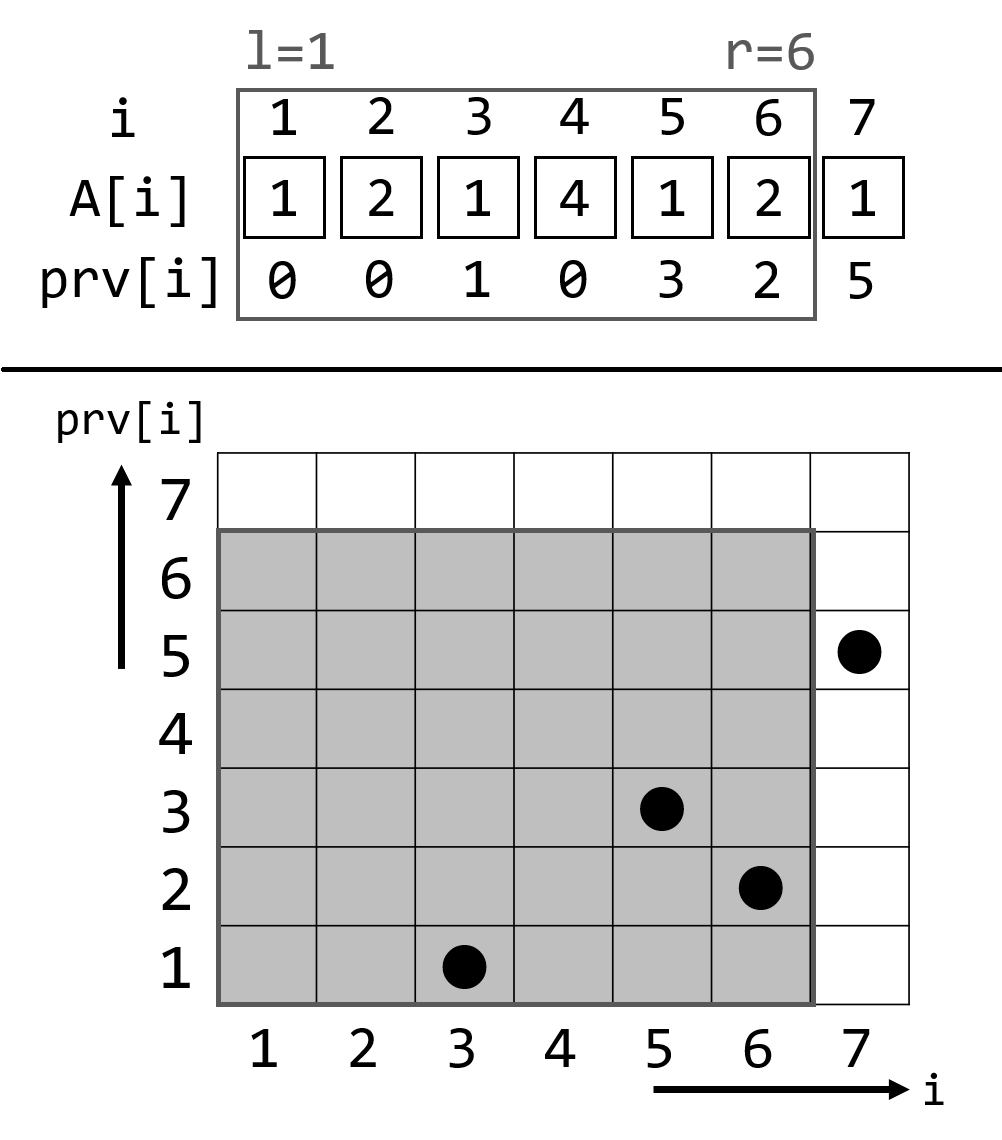
$[1,N] \times [1,N]$인 2차원 격자를 생성합니다. 처음에는 모든 칸에 0이 적혀 있습니다.

각 $i$에 대해, $prv[i]$를 $j < i$와 $A_j = A_i$를 만족하는 최대의 $j$ (저러한 $j$가 없으면 0)라고 정의합니다. 그리고 $prv[i] \neq 0$인 경우에만 좌표 $(i,prv[i])$의 값을 1 증가시킵니다.

이 때 $[L,R] \times [L,R]$ 정사각형의 합을 구하면, $[L,R]$ 구간에 한 번 이상 등장한 값마다 맨 왼쪽에서 등장한 인덱스 하나만을 제외하고 다른 모든 인덱스가 합에 정확히 1만큼을 기여하게 됩니다. 따라서 $[L,R]$ 구간의 서로 다른 수의 개수는 $(R-L+1)$에서 $[L,R] \times [L,R]$ 정사각형의 합을 뺀 것과 같습니다.

이제 다음 연산들을 수행하는 문제로 바뀌었습니다.

$i,j$가 주어지면, $(i,j)$ 좌표에 1을 더한다.
$l_1,r_1,l_2,r_2$가 주어지면, $l_1 \leq i \leq r_1, l_2 \leq j \leq r_2$를 만족하는 $(i,j)$ 좌표들의 값의 합을 구한다.

두 번째 연산은 다음과 같이 풀어 쓸 수 있습니다.

$l_1,r_1,l_2,r_2$가 주어지면,

$+$ ($i \leq r_1$과 $j \leq r_2$를 만족하는 $(i,j)$ 좌표들의 값의 합)

$-$ ($i \leq l_1-1$과 $j \leq r_2$를 만족하는 $(i,j)$ 좌표들의 값의 합)

$-$ ($i \leq r_1$과 $j \leq l_2-1$를 만족하는 $(i,j)$ 좌표들의 값의 합)

$+$ ($i \leq l_1-1$과 $j \leq l_2-1$를 만족하는 $(i,j)$ 좌표들의 값의 합)

을 구한다.

모든 연산을 $i$좌표의 오름차순으로 정렬하고 스위핑하면 1차원 문제로 바뀌므로, 펜윅 트리를 이용해서 구간 합을 구하면 $O((N+Q)\log{N})$ 시간복잡도에 해결됩니다.

구현

코드는 다음과 같습니다.

#include<bits/stdc++.h>
using namespace std;

int N, Q;
int last[1000001];
int A[100001], prv[100001], res[100001];

int fen[100001]; // 펜윅 트리
int Sum(int idx)
{
	int ret = 0;
	while(idx)
	{
		ret += fen[idx];
		idx &= idx-1;
	}
	return ret;
}
void Add(int idx, int val)
{
	while(idx <= N)
	{
		fen[idx] += val;
		idx += idx & -idx;
	}
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
	cin >> N;
	for(int i=1; i<=N; i++)
	{
		cin >> A[i];
		prv[i] = last[A[i]];
		last[A[i]] = i;
	}

	vector<array<int, 3> > q; // 연산 {i, j, k}들을 저장한다.
	// k = 0이면 (i,j) 좌표에 1을 더한다.
	// k > 0이면 [1,i] x [1,j] 직사각형의 합을 res[k]에 더한다.
	// k < 0이면 [1,i] x [1,j] 직사각형의 합을 res[k]에서 뺀다.
	for(int i=1; i<=N; i++)
		if (prv[i])
			q.push_back({i, prv[i], 0});

	cin >> Q;
	for(int i=1; i<=Q; i++)
	{
		int l, r;
		cin >> l >> r;
		res[i] = r-l+1;
		q.push_back({r, r, -i});
		q.push_back({r, l-1, i});
		q.push_back({l-1, r, i});
		q.push_back({l-1, l-1, -i});
	}

	// i의 오름차순으로, i가 같다면 업데이트가 먼저 나오는 순으로 정렬
	sort(q.begin(), q.end(), [&](const array<int, 3> &a, const array<int, 3> &b){
		if (a[0] != b[0]) return a[0] < b[0];
		return !!a[2] < !!b[2];
	});

	// 스위핑
	for(auto [i,j,k] : q)
	{
		if (k == 0) Add(j, 1);
		else if (k > 0) res[k] += Sum(j);
		else res[-k] -= Sum(j);
	}

	for(int i=1; i<=Q; i++)
		cout << res[i] << "\n";
	return 0;
}

온라인 $O((N+Q)\log{N})$

위에서 변환한 문제는 퍼시스턴트 세그먼트 트리(링크)를 이용하면 쿼리 정렬 과정 없이도 같은 시간복잡도에 해결할 수 있습니다. 링크한 글에 동일한 2D 구간합 문제의 풀이가 적혀 있으므로 생략하겠습니다.

업데이트가 있는 경우

다음 유형의 쿼리들이 중간에 섞여서 들어온다면 어떻게 해야 할까요?

$i,x$가 주어지면, $A[i]$를 $x$로 바꾼다.

펜윅 트리로 스위핑을 하는 풀이와 퍼시스턴트 세그먼트 트리 풀이 모두 중간에 업데이트를 빠르게 할 수 없다는 단점이 존재합니다.

반면에 2D 세그먼트 트리(링크) 등의 2차원 자료구조는 위의 모든 연산을 지원하므로 $O((N+Q)\log^2{N})$에 해결할 수 있습니다.

코드는 자료구조의 단순 구현 위주이므로 생략하겠습니다.

온라인 $O((N+Q)\sqrt[3]{N})$

“블럭 단위로 쪼개기” 아이디어와 “2차원 구간 합 문제로의 변환” 아이디어를 합쳐서 접근해 봅시다.

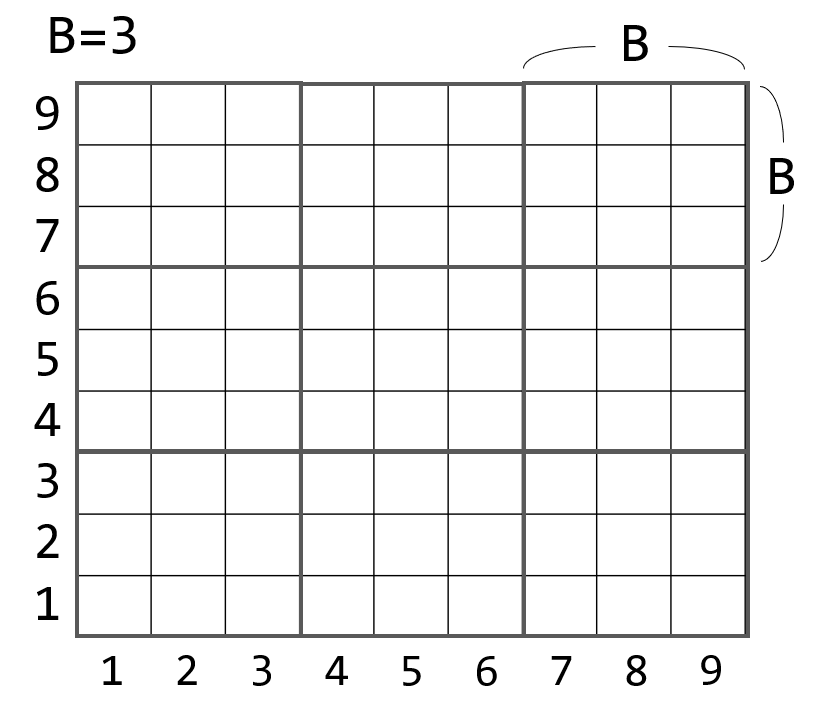
적당한 블럭 크기 $B$를 고정하면 2차원 격자를 $B \times B$ 크기의 $\left \lceil \frac{N}{B} \right \rceil \times \left \lceil \frac{N}{B} \right \rceil$개의 블럭들로 나누어서 생각할 수 있습니다. 쿼리가 들어오기 전에 블럭들의 2D prefix sum 배열을 $O((\frac{N}{B})^2)$의 시간복잡도와 공간복잡도로 전처리합시다.

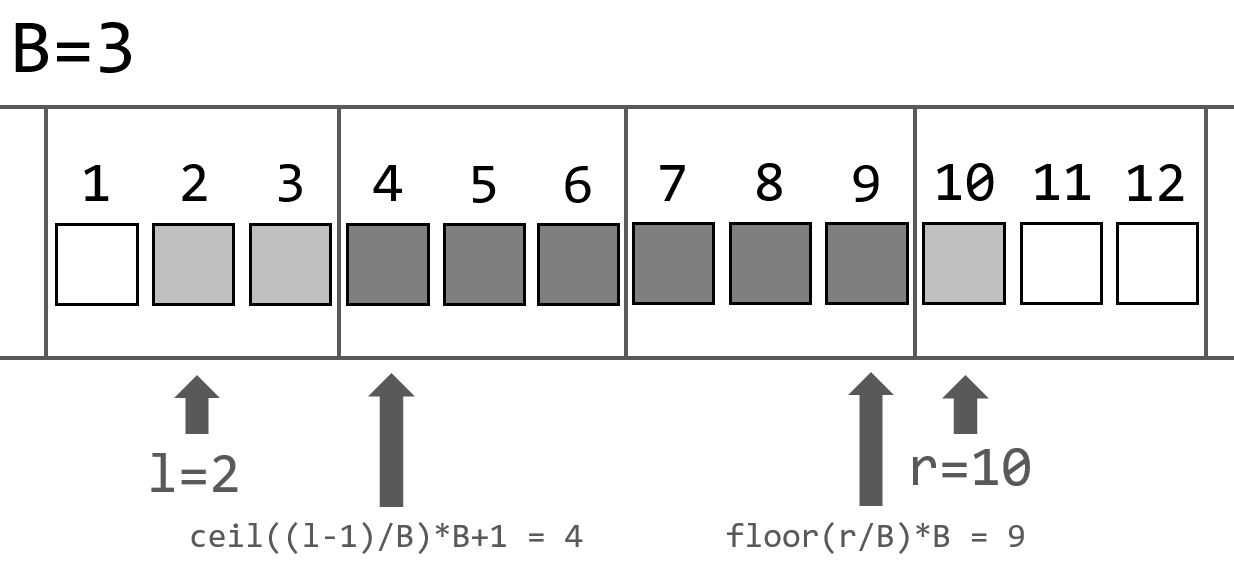
$[l,r]$ 구간의 서로 다른 수의 개수를 묻는 쿼리가 들어온다면, $[ \left \lceil \frac{l-1}{B} \right \rceil \cdot B+1, \left \lfloor \frac{r}{B} \right \rfloor \cdot B]$ 구간의 서로 다른 수의 개수는 2D prefix sum 배열을 통해 $O(1)$에 계산할 수 있습니다.

방금 계산한 부분을 제외한다면 양 끝에 길이가 $O(B)$인 구간만이 남게 되니, $[ \left \lceil \frac{l-1}{B} \right \rceil \cdot B+1, \left \lfloor \frac{r}{B} \right \rfloor \cdot B]$ 구간을 좌우로 한 칸씩 연장할 때 서로 다른 수의 개수를 $O(1)$에 관리할 수 있다면 쿼리당 $O(B)$에 문제가 해결됨을 알 수 있습니다.

각 $i$에 대해, $prv[i]$를 $j < i$와 $A_j = A_i$를 만족하는 최대의 $j$ (저러한 $j$가 없으면 0)이라고 정의합니다. 비슷하게, $nxt[i]$를 $j > i$와 $A_j = A_i$를 만족하는 최소의 $j$ (저러한 $j$가 없으면 $N+1$)이라고 정의합니다.

이 때, 다음과 같은 두 가지 상태 전이가 가능합니다.

$[l,r] \rightarrow [l-1,r]$로 이동할 때 $r < nxt[l-1]$이면 서로 다른 수의 개수가 1 증가
$[l,r] \rightarrow [l,r+1]$로 이동할 때 $prv[r+1] < l$이면 서로 다른 수의 개수가 1 증가

따라서 전체 문제가 해결됩니다.

최종 시간복잡도는 $O((\frac{N}{B})^2+QB)$가 되고, $B = \sqrt[3]{N}$으로 놓으면 $O((N+Q)\sqrt[3]{N})$이 됩니다.

이 풀이는 퍼시스턴트 세그먼트 트리 풀이에 비해 구현이 간단하고 메모리 사용량이 적으며, 상수가 작아서 더 빠르게 작동합니다.

구현

코드는 다음과 같습니다.

#include<bits/stdc++.h>
using namespace std;

const int B = 46, NB = 2174; // B, ceil(N/B)
int N, Q;
int last[1000001];
int A[100001], prv[100001], nxt[100001];
int S[2175][2175];

int main()
{
	ios::sync_with_stdio(0); cin.tie(0);
	cin >> N;
	for(int i=1; i<=N; i++)
		nxt[i] = N+1;
	for(int i=1; i<=N; i++)
	{
		cin >> A[i];
		prv[i] = last[A[i]];
		nxt[last[A[i]]] = i;
		last[A[i]] = i;

		if (prv[i]) S[(i-1)/B+1][(prv[i]-1)/B+1]++; // prv[i]=0일 때 음수 나눗셈이 안 나오게 잘 처리해야 한다.
	}
	// 2D prefix sum 전처리
	for(int i=1; i<=NB; i++)
		for(int j=1; j<=NB; j++)
			S[i][j] += S[i-1][j] + S[i][j-1] - S[i-1][j-1];

	cin >> Q;
	while(Q--)
	{
		int l, r;
		cin >> l >> r;

		int L = (l-1+B-1)/B*B+1, R = r/B*B, res = 0;
		int sql = (L-1)/B+1, sqr = (R-1+B)/B; // R=0일 때 음수 나눗셈이 안 나오게 잘 처리해야 한다.
		if (sql <= sqr) res = (R-L+1) - (S[sqr][sqr] - S[sqr][sql-1] - S[sql-1][sqr] + S[sql-1][sql-1]);
		else L = l, R = l-1; // 완전히 포함하는 블럭이 없는 경우

		while(l < L) if (R < nxt[--L]) res++; // [L,R] -> [L-1,R]
		while(R < r) if (prv[++R] < L) res++; // [L,R] -> [L,R+1]
		cout << res << "\n";
	}
	return 0;
}

$p \leq \sqrt{2 \cdot 10^5}$인 소수 $p$는 86개밖에 되지 않으므로 최댓값 세그먼트 트리를 86개 만들어서 해결할 수 있습니다.
$p > \sqrt{2 \cdot 10^5}$에서는 $0 \leq v_p \leq 1$이 성립하므로 서로 다른 수들의 곱을 구하는 문제로 변형할 수 있고, 서로 다른 수의 개수를 세는 문제와 비슷하게 풀립니다. (온라인 풀이가 강제되어 있음에 유의)

트리와 쿼리 9

정점 가중치 트리의 경로에 대한 서로 다른 수와 쿼리 문제입니다. 동일한 문제를 다룬 글(링크)이 있으니 읽어 보시기 바랍니다.

참고 자료

Codeforces box’s blog: [Tutorial] Square root decomposition and applications

서로 다른 수와 쿼리

개요

오프라인 $O(N\sqrt{Q})$

블럭 단위로 쪼개기

구현

오프라인 $O((N+Q)\log{N})$

2차원 구간 합 문제로의 변환

구현

온라인 $O((N+Q)\log{N})$

업데이트가 있는 경우

온라인 $O((N+Q)\sqrt[3]{N})$

구현

연습 문제

수열과 쿼리 5

서로 다른 수와 쿼리 1

서로 다른 수와 쿼리 2

Educational Codeforces Round 80 E. Messenger Simulator

USACO 2021 February Contest - Platinum. No Time to Dry

Codeforces Round #431 (Div. 1) C. Goodbye Souvenir

Codeforces Round #675 (Div. 2) F. Boring Queries

트리와 쿼리 9

참고 자료

Wireless Digital Communication 2

Introduction To Retroactivity