개요
트리에 관한 문제를 풀다 보면, 일부 정점만이 쿼리로 들어왔는데 모든 정점을 검사하기에는 비효율적인 경우가 있습니다. 이 때 필요 없는 정점과 간선들을 지워서 새로운 트리를 만드는 기법을 트리 압축이라고 부릅니다. 다른 말로는 Virtual Tree / Auxiliary Tree라고도 합니다.
다음 예시를 통해 트리 압축이 정확히 무엇인지와 어떻게 구현하는지에 대해서 살펴보겠습니다.
JOI Open Contest 2014. 공장들
정점이 $N$개인 간선 가중치 트리와 $Q$개의 쿼리가 주어집니다. $i$번 쿼리마다 서로소인 두 정점 부분집합 $S_i$와 $T_i$가 주어지면, $S_i$의 한 정점에서 $T_i$의 한 정점으로 가는 최단경로의 길이 중 가장 짧은 것을 찾아야 합니다. 다시 말해, $\min_{x \in S_i, y \in T_i} dist(x,y)$를 구해야 합니다. ($N \leq 5 \cdot 10^5, Q \leq 10^5, \sum \lvert S_i \rvert \leq 10^6, \sum \lvert T_i \rvert \leq 10^6$)
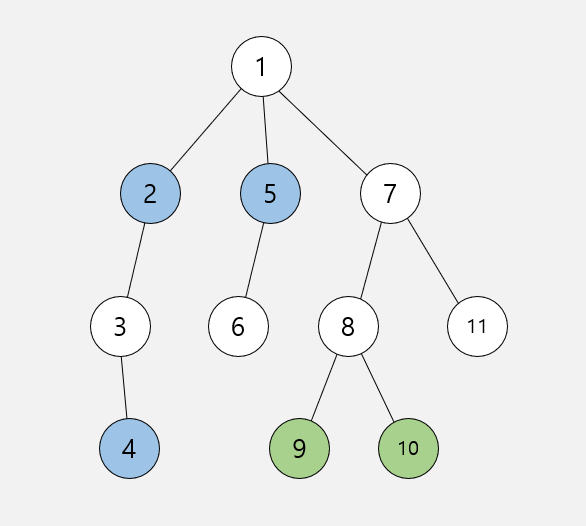
예를 들어 위 그림에서 집합 $S_i$의 정점들을 파란색으로, 집합 $T_i$의 정점들을 초록색으로 표기하고 모든 간선의 가중치를 1이라고 하면 이 쿼리의 정답은 4가 됩니다.
느린 풀이
각 쿼리당 $O(N)$에 해결하는 방법부터 생각해 봅시다.
- 정점 $x$에서 집합 $S_i$의 정점들 중 가장 가까운 정점과의 거리를 $s[x]$라 합시다.
- 정점 $x$에서 집합 $T_i$의 정점들 중 가장 가까운 정점과의 거리를 $t[x]$라 합시다.
$s,t$ 배열은 트리 DP로 계산할 수 있고, 정답은 $\min_{1 \leq x \leq N}(s[x] + t[x])$가 됩니다. 이 풀이는 $O(QN)$ 시간에 작동하기 때문에 전체 문제를 해결하기엔 아직 부족합니다.
빠른 풀이
$\lvert S_i \rvert$와 $\lvert T_i \rvert$가 작은 쿼리가 들어오는 경우를 생각해 보면, 위의 풀이에서 트리의 모든 정점을 매번 순회하는 과정이 비효율적임을 확인할 수 있습니다.
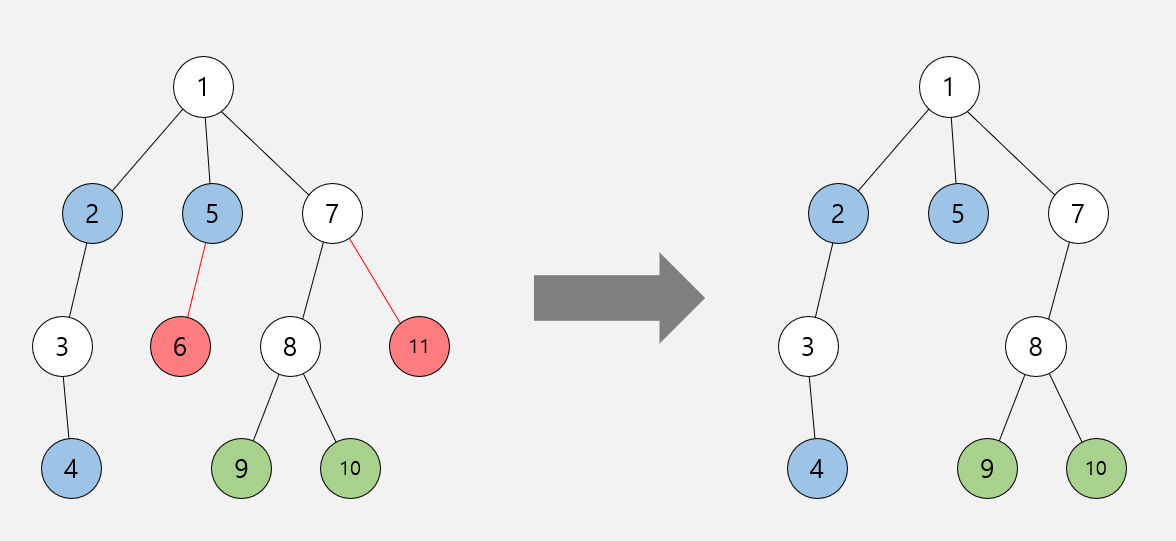
잘 생각해 보면 위 그림에서 빨간색 정점과 간선은 지워 버려도 영향을 주지 않습니다.
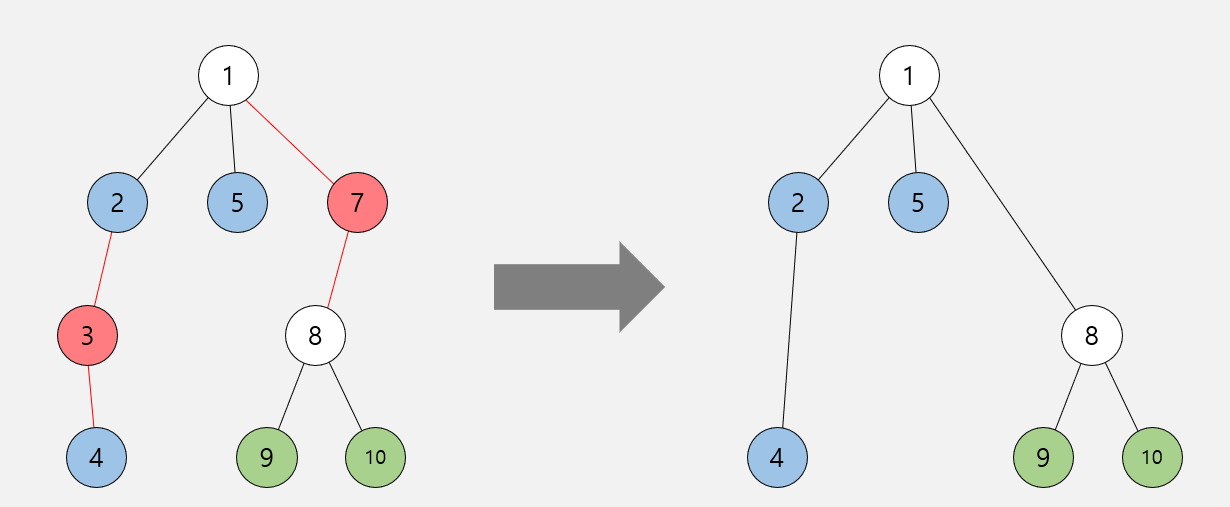
또한, 위 그림에서 빨간색 정점을 지운 뒤에 두 빨간 간선을 합쳐도 무방합니다.
쓸모 없는 정점과 간선들을 최대한 지우거나 합치면 트리의 최종적인 모습은 위 그림처럼 변하게 됩니다. 이렇게 트리의 크기를 줄여서 새로운 트리를 만드는 기법을 트리 압축이라 부르며, 작아진 트리에서 DP 풀이를 수행하면 빠르게 문제를 해결할 수 있습니다.
압축된 트리의 크기
$S_i \cup T_i$에 속하는 서로 다른 두 정점 $a,b$ 사이의 경로는 $LCA(a,b)$를 기준으로만 꺾이므로, 가능한 모든 정점 쌍들의 LCA의 집합을 $L_i$라 하면 새로 만들어질 트리의 정점들은 $S_i \cup T_i \cup L_i$로만 구성하면 됨을 알 수 있습니다. $L_i$의 크기의 상한은 어떻게 될까요?
정점 $x$가 Euler Tour에서 최초로 나타나는 위치를 $p[x]$라 합시다. 두 정점 $a,b$에 대해 일반성을 잃지 않고 $p[a] < p[b]$라 하면, $LCA(a,b)$는 Euler Tour 배열에서 $[p[a],p[b]]$ 구간의 정점들 중 level이 가장 작은 정점이 됩니다. (이 부분을 모르신다면 다음 글의 사전지식2 파트를 읽어 보시는 것을 추천합니다.)
위 사실에 의해, $S_i \cup T_i$ 내의 정점들을 $p[x]$가 작은 순으로 정렬했을 때 인접한 정점 쌍들의 LCA만 $L_i$에 추가하면 됨을 알 수 있습니다. 따라서 $L_i$의 크기의 상한은 $\lvert S_i \cup T_i \rvert - 1$이고, 각 쿼리당 $O(\lvert S_i \rvert + \lvert T_i \rvert)$ 크기의 트리가 만들어지게 됩니다.
트리 압축의 구현
지금까지의 내용을 정리하면 다음과 같습니다.
-
쿼리로 들어온 정점들을 Euler Tour 순서대로 정렬한 배열 $A$를 만듭니다.
-
$A$에서 인접한 정점 쌍들의 LCA를 모두 구해 $A$에 추가하고, 다시 Euler Tour 순서대로 정렬하고 중복을 제거합니다.
-
$A$에서 최초로 등장하는 정점이 새로운 트리의 루트가 되고, 인접한 두 정점을 $a,b$라 하면 $b$의 부모 정점이 $LCA(a,b)$가 됩니다. 이제 새로운 트리를 명시적으로 구성할 수 있습니다.
-
새로운 트리에서 정답을 구합니다.
Euler Tour를 구하고 LCA의 계산을 위한 스파스 테이블을 전처리하는 데에 $O(N \log N)$, 새로운 트리를 구성하는 데 $O(\sum (\lvert S_i \rvert + \lvert T_i \rvert) \log N)$의 시간이 소요되므로, 시간 제한 내에 전체 문제를 해결할 수 있습니다.
코드
코드는 다음과 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 4000000000000000000
#define ll long long
int N, Q;
vector<pair<int, int> > g[500001]; // 인접 리스트
int st[500001]; // 정점의 DFS preorder 순서
int h[500001]; // 정점의 level
ll D[500001]; // 정점에서 루트까지 가는 경로의 길이
int p[19][500001]; // 스파스 테이블
int type[500001]; // 현재 쿼리에서 정점이 어떤 집합에 속하는가?
vector<pair<int, ll> > G[500001]; // 압축된 트리
ll S[500001], T[500001]; // DP
ll res;
void DFS(int n, int prev)
{
static int ord = 0;
st[n] = ++ord;
h[n] = h[prev] + 1;
p[0][n] = prev;
for(auto [next,cost] : g[n])
{
if (next == prev) continue;
D[next] = D[n] + cost;
DFS(next, n);
}
}
int LCA(int a, int b)
{
if (h[a] < h[b]) swap(a, b);
int gap = h[a]-h[b];
for(int i=0; i<19; i++)
if (gap & 1<<i)
a = p[i][a];
if (a == b) return a;
for(int i=18; i>=0; i--)
if (p[i][a] != p[i][b])
a = p[i][a], b = p[i][b];
return p[0][a];
}
void DFS2(int n)
{
S[n] = T[n] = INF;
if (type[n] == 1) S[n] = 0;
else if (type[n] == 2) T[n] = 0;
for(auto [next,cost] : G[n])
{
DFS2(next);
S[n] = min(S[n], S[next] + cost);
T[n] = min(T[n], T[next] + cost);
}
// 현재 시점에서
// S[n] : n의 서브트리에서 n과 가장 가까운 type=1 정점과의 거리
// T[n] : n의 서브트리에서 n과 가장 가까운 type=2 정점과의 거리
// 가 된다.
}
void DFS3(int n, ll s, ll t)
{
// 현재 시점에서
// s : n의 부모 정점 p와 가장 가까운 type=1 정점과의 거리 + cost(n, p)
// t : n의 부모 정점 p와 가장 가까운 type=2 정점과의 거리 + cost(n, p)
// 가 된다.
s = min(s, S[n]);
t = min(t, T[n]);
// 현재 시점에서
// s : n과 가장 가까운 type=1 정점과의 거리
// t : n과 가장 가까운 type=2 정점과의 거리
// 가 된다.
res = min(res, s + t);
for(auto [next, cost] : G[n])
DFS3(next, s + cost, t + cost);
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin >> N >> Q;
for(int i=0; i<N-1; i++)
{
int a, b, c;
cin >> a >> b >> c;
a++; b++; // 1-based
g[a].push_back({b, c});
g[b].push_back({a, c});
}
// Euler Tour와 LCA 전처리
DFS(1, 0);
for(int i=1; i<19; i++)
for(int j=1; j<=N; j++)
p[i][j] = p[i-1][p[i-1][j]];
while(Q--)
{
vector<int> A;
int s, t, x, y;
cin >> s >> t;
while(s--)
{
cin >> x;
x++; // 1-based
A.push_back(x);
type[x] = 1;
}
while(t--)
{
cin >> y;
y++; // 1-based
A.push_back(y);
type[y] = 2;
}
// 1. Euler Tour 순으로 정렬하기
sort(A.begin(), A.end(), [&](int a, int b){ return st[a] < st[b]; });
// 2. 인접한 정점 쌍들의 LCA를 추가하기
int sz = A.size();
for(int i=1; i<sz; i++)
A.push_back(LCA(A[i-1], A[i]));
sort(A.begin(), A.end(), [&](int a, int b){ return st[a] < st[b]; });
A.erase(unique(A.begin(), A.end()), A.end());
// 3. 압축된 트리를 명시적으로 구성하기
for(int i=1; i<A.size(); i++)
{
int prev = LCA(A[i-1], A[i]), n = A[i];
G[prev].push_back({n, D[n]-D[prev]});
}
// 4. 새로운 트리에서 정답 구하기
res = INF;
DFS2(A[0]);
DFS3(A[0], INF, INF);
cout << res << "\n";
// 다음 쿼리를 위한 초기화
for(int n : A)
{
type[n] = 0;
G[n].clear();
}
}
return 0;
}
연습 문제
JOI Open Contest 2014. 공장들
위에서 설명한 문제입니다.
ACM-ICPC Asia Tsukuba Regional Contest 2017. Counting Cycles
아무 정점을 루트로 고정하고 DFS Tree를 만들면 최대 16개의 역방향 간선이 존재하고, 각각의 역방향 간선마다 트리 상의 경로 하나와 결합해서 사이클을 하나씩 만들 수 있습니다. 이들을 기초 사이클이라 부르면, 모든 사이클은 기초 사이클들의 간선들의 XOR을 통해 만들 수 있음이 알려져 있습니다. cycle basis 참조
기초 사이클 부분집합이 최대 $2^{16}$개이므로 이들을 단순히 열거해 보는 $2^{16} \cdot (N+M)$ 풀이를 생각할 수 있지만 시간 제한 안에 풀기에는 어렵습니다. 하지만 역방향 간선의 끝점인 정점들과 이들의 LCA만 남기는 트리 압축을 수행하면 정점이 63개, 간선이 78개 이하로 줄어들어 위의 완전 탐색 풀이로 해결할 수 있습니다.
코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
int N, M;
vector<int> g[100001];
bool vis[100001];
int st[100001], h[100001], p[17][100001];
vector<pair<int, int> > backedge;
vector<int> A;
int pp[100001]; // 압축된 트리의 부모
map<pair<int, int>, int> ord; // 간선 -> 번호
pair<int, int> edg[78]; // 번호 -> 간선
bitset<78> cycle[16]; // 기초 사이클들의 XOR로 만들어진 간선 리스트
vector<int> G[100001]; // 기초 사이클들의 XOR로 만들어진 그래프
void DFS(int n, int prev)
{
static int ord = 0;
vis[n] = true;
st[n] = ++ord;
h[n] = h[prev] + 1;
p[0][n] = prev;
for(int next : g[n])
{
if (next == prev) continue;
if (vis[next])
{
if (h[n] > h[next]) // 역방향 간선 발견
{
backedge.push_back({n, next});
A.push_back(n);
A.push_back(next);
}
continue;
}
DFS(next, n);
}
}
int LCA(int a, int b)
{
if (h[a] < h[b]) swap(a, b);
int gap = h[a]-h[b];
for(int i=0; i<17; i++)
if (gap & 1<<i)
a = p[i][a];
if (a == b) return a;
for(int i=16; i>=0; i--)
if (p[i][a] != p[i][b])
a = p[i][a], b = p[i][b];
return p[0][a];
}
void DFS2(int n) // 컴포넌트 방문 체크
{
vis[n] = true;
for(int next : G[n])
{
if (vis[next]) continue;
DFS2(next);
}
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin >> N >> M;
for(int i=0; i<M; i++)
{
int a, b;
cin >> a >> b;
g[a].push_back(b);
g[b].push_back(a);
}
// Euler Tour와 LCA 전처리, backedge들 구하기
DFS(1, 0);
for(int i=1; i<17; i++)
for(int j=1; j<=N; j++)
p[i][j] = p[i-1][p[i-1][j]];
// 트리 압축
// 1. Euler Tour 순으로 정렬하기
sort(A.begin(), A.end(), [&](int a, int b){ return st[a] < st[b]; });
A.erase(unique(A.begin(), A.end()), A.end());
// 2. 인접한 정점 쌍들의 LCA를 추가하기
int sz = A.size();
for(int i=1; i<sz; i++)
A.push_back(LCA(A[i-1], A[i]));
sort(A.begin(), A.end(), [&](int a, int b){ return st[a] < st[b]; });
A.erase(unique(A.begin(), A.end()), A.end());
// 3. 압축된 트리의 부모 배열 만들기
for(int i=1; i<A.size(); i++)
{
int prev = LCA(A[i-1], A[i]), n = A[i];
pp[n] = prev;
}
// 4. 새로운 트리에서 정답 구하기
int E = 0; // 간선의 개수
for(int i=0; i<backedge.size(); i++) // 기초 사이클들 구하기
{
auto [a,b] = backedge[i];
auto insert = [&](int x, int y) // 간선 번호 매기기
{
if (ord.find({x, y}) == ord.end())
{
ord[{x, y}] = E;
edg[E] = {x, y};
E++;
}
cycle[i][ord[{x, y}]] = true;
};
insert(a, b);
while(a != b) // backedge를 타고 올라가기
{
insert(pp[a], a);
a = pp[a];
}
}
// 최대 2^16가지 사이클 후보들을 완전 탐색
memset(vis, 0, sizeof(vis));
int res = 0;
for(int i=1; i<(1<<backedge.size()); i++)
{
bitset<78> bs;
for(int j=0; j<backedge.size(); j++)
if (i & 1<<j)
bs ^= cycle[j];
// 기초 사이클들의 XOR로 만들어진 그래프 구성하기
vector<int> v;
for(int j=0; j<78; j++)
if (bs[j])
{
auto [a,b] = edg[j];
v.push_back(a);
v.push_back(b);
G[a].push_back(b);
G[b].push_back(a);
}
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
// simple cycle인가?
// = 모든 정점의 degree가 0 또는 2이면서 컴포넌트가 하나인가?
DFS2(v[0]);
int die = 0;
for(int n : v)
if (G[n].size() != 2 || vis[n] == false)
die = 1;
if (!die) res++;
// 초기화
for(int n : v)
{
vis[n] = false;
G[n].clear();
}
}
cout << res << "\n";
return 0;
}
아래 문제들은 트리 압축을 생각한 뒤의 풀이가 어렵지 않으므로, 직접 풀어 보시는 것을 추천드립니다.