도형의 합집합과 넓이

도형의 불리언 연산이란, 여러 도형의 영역에 대한 집합 연산을 말합니다.

두 원의 교집합의 넓이를 구하는 방법은 잘 알려져 있습니다. 부채꼴 2개의 넓이를 합친 다음, 이등변삼각형 2개의 넓이를 빼는 방식으로 구할 수 있습니다. 같은 방법으로 두 원의 합집합의 넓이도 구할 수 있습니다. 하지만 원이 3개만 되어도 이런 “포함 배제” 접근을 하기 어렵습니다.

이 글에서는 도형의 합집합 및 그 넓이를 구하는 일반적인 방법을 소개합니다.

테두리 따기

아래 그림에서 테두리가 갖고 있는 중요한 성질을 찾아봅시다.

테두리는 도형의 둘레로 이루어져 있습니다.

그런데 이뿐만이 아닙니다. 도형의 둘레 중 다른 도형의 내부에 포함되지 않는 부분만이 테두리가 됩니다.

도형의 합집합의 테두리를 구하는 방법은 다음과 같습니다.

도형 사이의 모든 교점을 구합니다.
각 도형마다 둘레를 다른 도형들과의 교점으로 분할합니다. 분할한 각 부분을 “조각”이라고 부릅시다.
- 위 그림에서 예를 들어보면, 맨 아래의 원은 네 조각으로 분할되어 있습니다.
- 원의 경우, 교점들을 각도 순으로 정렬하면 됩니다.
- 다각형의 경우, 우선 꼭짓점으로 분할하고, 각 변마다 그 위의 교점들을 정렬하면 됩니다.
각 조각마다, 원래 자신이 속했던 도형을 제외하고 나머지 중 적어도 하나의 내부에 포함되는지 판별합니다. 포함되지 않는다면 그 조각은 테두리의 일부가 됩니다.
- 꼭 조각 전체를 생각할 필요는 없고, 조각 위의 한 점을 잡아서 점이 도형 내부에 속하는지 판별해도 됩니다.

모든 도형이 원일 경우, 교점은 $O(n^2)$개이므로 조각도 $O(n^2)$개이고, 각 조각이 테두리를 이루는지 $O(n)$에 판별할 수 있으므로 전체 시간 복잡도는 $O(n^3)$입니다.

Java에서의 사용

Java에는 이 기능이 내장되어 있습니다. 합집합만이 아니라 교집합, 차집합, 대칭차집합 등을 지원합니다.

도형은 java.awt.geom에 있는 클래스 Path2D, Ellipse2D 등으로 만들고 Area로 관리합니다. 만든 Area의 테두리를 PathIterator로 따올 수도 있습니다.

Area A = new Area();  // 빈 Area를 만듦

Path2D.Double p = new Path2D.Double();
p.moveTo(a, b); // 커서를 이동
p.lineTo(a, b); // 커서를 이동시키면서 선분을 그림
p.closePath();

Area A2 = new Area(p); // Path2D로부터 Area를 만듦
A.add(A2); // A에 A2를 합집합

PathIterator it = area.getPathIterator(null);
while (!it.isDone()) {
  switch (it.currentSegment(tmp)) {
    case PathIterator.SEG_MOVETO: ...
    case PathIterator.SEG_LINETO: ...
    case PathIterator.SEG_CLOSE: ...
  }
  it.next();
}

자세한 내용은 공식 문서를 참조하세요.

넓이 구하기

그린 정리(Green theorem)¹는 닫힌 곡선에 대한 면적분을 선적분으로 바꿔주는 정리입니다.

$C$를 조각마다 매끄러운 단순 닫힌 곡선이라고 합시다.
- “조각마다 매끄러운”은 무한 번 미분 가능한 곡선을 여러 개 이어붙인 형태를 의미합니다.
- “단순”은 자기 자신과 교차하지 않음을 의미합니다.
- “닫힌”은 출발했던 점으로 돌아옴을 의미합니다.
- 이러한 곡선의 예로 원이나 단순다각형이 있습니다. 단순다각형의 경우 선분이 무한 번 미분 가능한 곡선이고, 그 선분을 여러 개 이어붙인 형태이기 때문에 조각마다 매끄러운 곡선입니다.
$D$를 그 곡선의 내부 영역이라고 합시다.
$L$과 $M$이 $(x, y)$에 대한 함수라고 합시다. 여기에도 조건이 더 붙지만 이 글에서는 필요하지 않습니다.

그러면 $C$를 반시계 방향으로 돌면서 선적분($\oint$)을 한다고 할 때 다음이 성립합니다.

\[\oint_C(L\ dx+ M\ dy) = \iint_D(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}) \ dx \ dy\]

이것으로 면적을 어떻게 구할 수 있을까요? 면적은 다음과 같습니다.

\[\iint_D 1 \ dx \ dy\]

따라서 $\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y} = 1$이 되도록 $M$과 $L$을 잡아주면 됩니다. 대표적으로 $M = \frac{x}{2}$, $L = -\frac{y}{2}$를 사용하고, 이때 그린 정리는 이렇게 바뀝니다.

\[\frac{1}{2} \oint_C(x\ dy - y\ dx) = \iint_D 1 \ dx \ dy\]

이제 우리가 원하는 곡선 $C$를 잡아준 다음 선적분을 열심히 계산하면 됩니다.

원 하나

우선 중심이 $(x_c, y_c)$, 반지름이 $r$인 원 하나의 넓이를 구해봅시다. 그러려면 $C$를 $\theta$에 대한 매개변수 곡선으로 나타내면 됩니다. 즉 $x = x_c + r \cos \theta$, $y = y_c + r \sin \theta$, $0 \leq \theta < 2 \pi$입니다. 이제,

연쇄 법칙(chain rule)에 의해 $\oint (x\ dy - y\ dx) = \oint (x \frac{dy}{d\theta} d\theta - y \frac{dx}{d\theta} d\theta)$
$\frac{dy}{d\theta} = r \cos \theta$
$\oint x \frac{dy}{d\theta} d\theta = \oint (x_c + r \cos \theta)(r \cos \theta) d\theta = r \oint (x_c \cos \theta + r \cos^2 \theta) d\theta$
$-\oint y \frac{dx}{d\theta} d\theta = \oint (y_c + r \sin \theta)(r \sin \theta) d\theta = r \oint (y_c \sin \theta + r \sin^2 \theta) d\theta$
$\frac{1}{2} \oint (x \frac{dy}{d\theta} d\theta - y \frac{dx}{d\theta} d\theta) = \frac{r}{2} \oint (x_c \cos \theta + y_c \sin \theta + r) d\theta$

따라서 적분 결과는 $\frac{r}{2}(x_c \sin \theta - y_c \cos \theta + r\theta) + C$입니다. 실제로 $\theta$에 $0$과 $2\pi$를 넣어서 빼보면 원의 넓이인 $\pi r^2$만 남는 것을 확인할 수 있습니다.

한편, $a \leq \theta \leq b$에 해당하는 부채꼴 영역의 넓이를 구하려고 $\theta$에 $a$와 $b$를 넣어서 빼보면 이상한 값이 나오는데, 이는 부채꼴 영역이 호 하나만 있는 게 아니라 선분 두 개가 더 있기 때문입니다. 따라서 선분에 대해서도 선적분을 해줘야 합니다. 이에 대해서는 후술합니다.

원 두 개

테두리가 호 두 개로 이루어져 있다고 해봅시다. 그러면 각각의 호를 매개변수 곡선으로 생각할 수 있습니다. 호의 매개변수 곡선은 위와 별반 다르지 않습니다. 방정식은 원과 같은데, $\theta$의 범위만 다릅니다.

이제 그린 정리를 여기에도 적용하려면 매개변수 곡선 두 개를 이어붙여 하나의 매개변수 곡선으로 만들어야 합니다. 그러려면 곡선의 방정식을 어떻게 바꿔야 할까요?

안 바꿔도 됩니다.

좀 더 단순화해서, 함수 $y = f_1(x)$ ($l_1 \leq x \leq r_1$), $y = f_2(x)$ ($l_2 \leq x \leq r_2$) 두 개를 이어붙여 만든 함수 ($l_1 \leq x \leq r_1 + r_2 - l_2$)를 적분한다고 해봅시다. 그러면 그 함수는

$x \leq r_1$이면 $y = f_1(x)$
아니면 $y = f_2(x - r_1 + l_2)$

가 됩니다. 그런데 $\int_{r_1}^{r_1 + r_2 - l_2} f_2(x - r_1 + l_2) dx = \int_{l_2}^{r_2} f_2(x) dx$라서, 그냥 두 함수를 따로 적분하고 합하면 됩니다. 직관적으로, 함수를 $x$ 방향으로 평행이동한 것이라서 적분값이 달라질 리가 없습니다.

매개변수 곡선도 마찬가지입니다. 곡선들을 모아 하나의 큰 곡선으로 만들 필요 없이, 곡선 각각을 적분하고 합치면 됩니다.

원 여러 개

원이 여러 개 있을 때로 절차를 확장하면 다음과 같습니다.

원의 합집합의 테두리를 이루는 호를 모두 구합니다.
각 호에 대해 그린 정리를 적용해서 합칩니다.

네, 이게 끝입니다. 매우 복잡한 디테일이 있을 것 같이 생겼지만 그렇지 않습니다.

첫째로 들 수 있는 의문점은 “테두리를 ‘순서대로’ 따라가면서 적분해야 하지 않나?”일텐데요, 그렇지 않습니다. 테두리의 모든 부분을 한 번씩 지나가기만 하면 됩니다. 즉, 적분을 할 호를 선택하는 순서는 중요하지 않습니다.

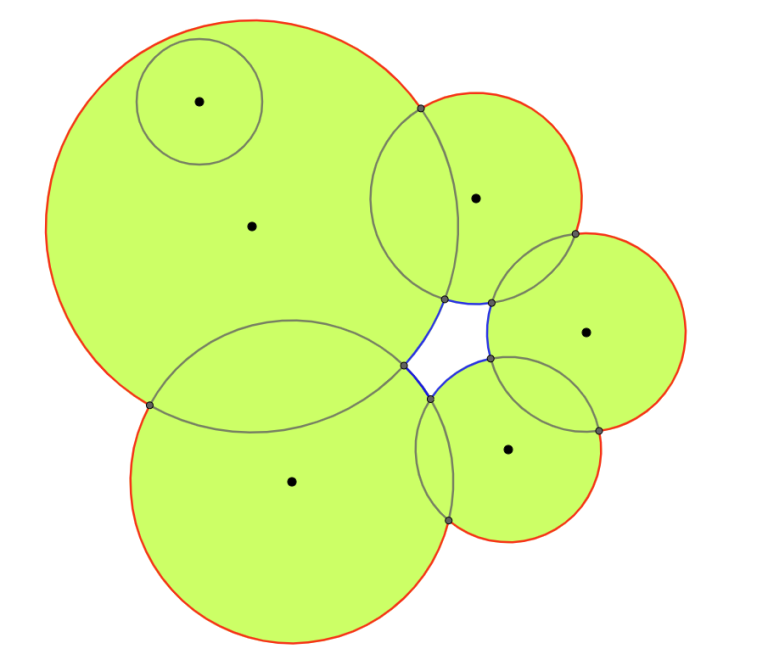
둘째로 “구멍이 있으면 이상해지지 않을까?”라는 의문이 들 수 있습니다. 다행히도 구멍이 얼마나 있든 넓이는 잘 계산됩니다. 왜냐하면 그 구멍은 시계방향으로 돌게 되어서, 자연스럽게 음의 넓이로 계산되기 때문입니다. 아래 그림에서 빨간색 테두리는 반시계방향으로 도는 부분, 파란색 테두리는 시계방향으로 도는 부분입니다. 원의 둘레를 반시계방향으로 돌 때 파란색 테두리에서 어떻게 되는지 확인해 보세요.

선분이 포함된 도형

다각형이나 부채꼴처럼 둘레에 선분이 포함될 경우, 꼭짓점을 기준으로 분할해서 선분 단위로 생각하면 편합니다.

선분은 매개변수 곡선 $x = x_c + v_x t$, $y = y_c + v_y t$, $0 \leq t \leq 1$로 표현할 수 있습니다.

연쇄 법칙(chain rule)에 의해 $\oint (x\ dy - y\ dx) = \oint (x \frac{dy}{dt} dt - y \frac{dx}{dt} dt)$
$= \oint(v_y (x_c + v_x t)dt - v_x (y_c + v_y t)dt)$
$= \oint(v_y x_c - v_x y_c)dt$
$= (v_y x_c - v_x y_c)t + C$

$t$에 0과 1을 넣어서 빼면 그냥 $v_y x_c - v_x y_c$가 됩니다.

문제 풀이

BOJ 17804

BOJ 17804 Knocked Ink는 잉크가 원형으로 퍼질 때, 합집합의 넓이가 특정 값이 되는 순간을 구하는 문제입니다.

원의 합집합의 넓이는 시간에 따른 증가함수이기 때문에 이분탐색으로 답을 구할 수 있습니다.

ojuz 색종이

ojuz 색종이는 색종이를 놓을 때마다 각 색종이가 보이는 영역의 넓이를 구하는 문제입니다. 서브태스크 1에서는 모든 색종이가 원이고, 2에서는 원 또는 삼각형입니다.

$A_{i,j}$를 첫 $i$개의 색종이를 놓았을 때 $j$번째 색종이가 보이는 영역의 넓이라고 합시다. 즉 우리가 구해야 하는 값은 모든 $A_{i,j}$입니다. $i = j$일 때는 그냥 도형 하나의 넓이를 구해주면 됩니다.

$S_{l,r}$을 $l$번째부터 $r$번째까지의 색종이를 놓았을 때 전체 영역의 넓이라고 합시다. 그러면 $i < j$일 때 $A_{i,j} = S_{j,i} - S_{j+1,i}$입니다.

모든 $A$ 값 대신에 모든 $S$ 값을 구해줍시다. 일단 색종이를 다 놓은 다음 모든 도형의 둘레를 조각으로 나눕니다. 그 다음 각 조각 및 모든 $l \leq r$에 대해, 그 조각이 $S_{l,r}$의 테두리를 이룰 경우 그 조각에 대한 적분값을 $S_{l, r}$에 더합니다. 도형 $k$로부터 나온 조각 하나가 $S_{l,r}$의 테두리를 이루려면

물론 $l \leq k \leq r$이어야 합니다.
도형 $k$를 놓는 순간 그 조각이 테두리에 있어야 합니다. 즉 도형 $l, \cdots, k-1$ 바깥에 그 조각이 있어야 합니다.
도형 $r$을 놓을 때까지 그 조각이 테두리에 남아있어야 합니다. 즉 도형 $k+1, \cdots, r$ 바깥에 그 조각이 있어야 합니다.

$S_{l, r}$에 대한 표를 그려본다고 생각하면 각 조각이 영향을 미치는 $S$들은 직사각형을 이루기 때문에, 누적합으로 각 $S$를 계산할 수 있습니다.

주의할 점은 여러 조각이 완전히 일치할 수도 있다는 것입니다. 예를 들어 두 원이 완전히 일치하거나, 두 삼각형의 둘레가 선분으로 겹칠 수 있습니다. 이 경우 나중에 나타난 조각이 우위를 점하고 이전에 나타난 조각은 사라집니다. 그래서 각 조각이 $S_{l,r}$의 테두리를 이루는지 판별할 때 주의를 기울여야 합니다.

아쉽게도 서브태스크 1만 해도 구현량이 상당하기 때문에 서브태스크 1 코드만 첨부합니다.

BOJ 9598

BOJ 9598 Cleaning the Hallway는 도넛의 합집합의 넓이를 구하는 문제입니다.

도넛의 바깥쪽 원은 반시계방향으로 돌고, 안쪽 원은 시계방향으로 돌면 됩니다. 나머지는 원의 합집합과 동일합니다. 교점을 구하고 조각으로 나눈 다음 그린 정리를 써주되, 테두리를 구할 때는 조각이 도넛의 안에 속하는지 판별하면 됩니다.

~~참고로 전 안 풀었습니다.~~

참고 자료

이 정리를 만든 수학자 George Green을 따서 이름이 붙었습니다. ↩