Exploring Simulated Annealing for Derivative-free Optimization 2
Exploring Simulated Annealing for Derivative-free Optimization 2
이전 포스트 Exploring Simulated Annealing for Derivative-free Optimization 1에 이어서 기존 Simulated Annealing을 여러 방면으로 개선시킨 방법론들에 대해 이야기하겠습니다.
Fast Simulated Annealing
기존의 온도 쿨링의 경우, 쿨링되는 과정이 너무 느려서 실제로 converge할 때까지 시간이 너무 오래걸린다는 단점이 있습니다. 이러한 문제를 해결하기 위해서 새롭게 제안된 방법이 바로 Fast Simulated annealing입니다.
기존의 SA의 경우, 새로운 상태를 채택할지에 대한 확률을 exponential function을 통해서 결정했습니다. 즉, exponential function을 사용하기 때문에, 새로운 상태의 energy가 기존에 비해 꽤나 높을 경우, 새 상태를 채택할 확률이 굉장히 빠르게 감소하였습니다.
그러나 FSA의 경우, 다음과 같은 형태의 함수를 사용합니다.
- $y_{k} = (\frac{E(y_{k}) - E(x_{k})}{kT_{k}})$
- $p_{k} = q(y_{k})$
즉, 우리가 기존에 exponentional function을 사용하던 형태에서, 이제는 새로운 함수 커널인 q를 사용하는 것으로 새로운 확률 분포식을 사용하게 됩니다. 이 때에 사용하는 함수 q의 경우는, new state와 current state 사이의 에너지 차이가 클 때에도 exponential function보다 감소율이 작은 함수를 사용합니다.
(대표적인 예시로 $q(x) = \frac{1}{1 + x}$ 함수를 사용합니다)
이를 통해서 많은 state들에 대한 acceptance가 증가하게 되기 때문에, 우리가 진행하는 동안의 temperature decaying 수치를 늘려서 온도가 빠르게 감소하도록 만들 필요가 있습니다.
이를 위해서 FSA에는 다음과 같은 형태의 Convergence Theorem이 사용됩니다.
Convergence of FSA
f를 주어진 범위 X 내에 위치하는 고립된 전역 최적값 집합이라 가정하겠습니다. 또한, f가 국지적으로 $C^{3}$이며 f의 Hessian이 positive definite일 때, $\gamma \in (0, 1], $에 대해
- $T_{k} = \frac{1}{(k+1)^{\gamma}log( (k+1)^{ \gamma } )}$
를 만족합니다.
또한, 특정 포인트의 neighbor point를 생성하는 마르코브 커널 G가 ergodicity를 만족한다고 가정할 때, for $q(x) = \frac{1}{1 + x}$, there exists $C_{\epsilon} > 0$ s.t.
- $P(x_{k}) >= 1 - \frac{C_{\epsilon}}{(k+1)^{\gamma}}$
위 결과가 의미하는 것은, 앞서서 SA에서 μ가 iteration을 거듭할수록 1에 가까워질 수 있다는 것을 보인 theorem처럼 실제로 FSA가 어떻게 convergence 할 수 있는지에 대한 정보를 제공합니다.
SA에서 사용하던 T의 경우는, 기존의 iteration이 반복할 때에도 줄어드는 속도가 굉장히 작은 logarithm을 분모로 두고 있는 함수였습니다.
그러나 이제는 주어진 k에 대해서, 분모에 k에 대한 항이 한 번 더 곱해지는 형태로 식이 바뀌게 됩니다. 그렇기 때문에, 우리가 특정 $\gamma$를 어떻게 선택하는지에 따라서 달라지기는 하지만, 주어진 식이 수렴하는 속도가 inverse logarithm에 비해서는 iteration의 수가 커짐과 동시에 훨씬 더 빠르게 수렴한다는 것을 알 수 있습니다.
이에 따라서 실제로 기존의 SA보다는 수학적으로 더 빠르게 동작한다는 것을 알 수 있으며, 우리가 실제로 고려하는 convergence 또한 보장된다는 것이 분명하게 됩니다. 그렇기에 FSA는 우리가 주어진 objective function 및 temperature decaying을 조정하는 것으로 Simulated annealing을 더욱 최적화하거나 변형시킬 수 있다는 것을 보여줍니다.
FSA - example
Rosenbrock Function
기존과 동일한 하이퍼파라미터 세팅에서 실행한 결과입니다.
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from ipywidgets import interactive
import random
import math
def rosenbrock(x, y, a = 1, b = 100):
return (a - x)**2 + b*((y - x**2)**2)
a = 1
b = 100
r = 0.1
bc = 10
T1 = 1
T2 = 1
seed = 2
max_iteration = 100
f = rosenbrock
random.seed(seed)
x1 = np.linspace(-2, 2)
x2 = np.linspace(-1, 3)
X1, X2 = np.meshgrid(x1, x2)
F = rosenbrock(X1, X2, a, b)
x = [-2.0, -1.0, 2.0, 3.0]
y = [-2.0, 2.0, -2.0, 2.0]
X = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
Y = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
best = [20000, 20000, 20000, 20000]
best_point = [(10, 10), (10, 10), (10, 10), (10, 10)]
def G(x, y, r):
a, b = random.uniform(-r, r), random.uniform(-r, r)
return x+a, y+b
def sa_p(E, bc, T):
return np.exp(-(E / (bc * T)))
def fsa_p(E, bc, T):
E = max(E, 0)
return 1 / (1 + (E / (bc * T)))
def plotter(E, A):
global X, Y
fig = plt.figure(figsize = [12, 8])
ax = plt.axes(projection='3d')
ax.plot_surface(X1, X2, F, cmap='jet', alpha=0.8)
ax.view_init(elev=E, azim=A)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('F(X, Y)')
for i in range(4): #FSA
ax.scatter(X[max_iteration][1][i], Y[max_iteration][1][i], f(X[max_iteration][1][i], Y[max_iteration][1][i], a, b), color = 'limegreen')
for i in range(4):
for j in range(4):
X[0][i][j] = x[j]
Y[0][i][j] = y[j]
for k in range(max_iteration):
T1 = 1 / math.log(k+2)
T2 = 1 / ((k + 1) * math.log(k+2))
for j in range(4): #FSA
x, y = X[k][1][j], Y[k][1][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[1]:
best[1] = min(best[1], fy)
best_point[1] = (nx, ny)
p = fsa_p(fy - fx, bc, T2)
now = random.uniform(0, 1)
if now < p:
X[k+1][1][j], Y[k+1][1][j] = nx, ny
else:
X[k+1][1][j], Y[k+1][1][j] = x, y
print('iteration %d - best score: %f / point (x, y) = (%f, %f)'%(k, best[1], best_point[1][0], best_point[1][1]))
print('\n\nlegend\n')
print('FSA - limegreen points')
iplot = interactive(plotter, E = (-20, 90, 5), A = (-20, 90, 5))
iplot

Sequential Monte Carlo Simulated Annealing
기존의 FSA가 SA에서 temperature decaying part를 변형하고 실제 probability 계산을 볼츠만 분포에서 다른 커널 q를 사용하여, 여러 차례의 시도를 훨씬 더 적은 시도 안에 끝낼 수 있도록 변경하였다면, SMC-SA의 경우, 기존에 우리가 사용하던 볼츠만 분포를 그대로 사용하는 형태에서 SA를 변형시킨 방법입니다.
그러나 이는 SA와 FSA 모두가 가지고 있던 문제점에 대해서 지적하면서, 이를 개선하기 위한 새로운 방향성을 제시합니다.
기존의 SA의 경우, 하나의 initial point에 대해서, 그 지점에서부터 시작하는 iteration들을 거듭하면서 최적의 지점을 찾아나가는 방식으로 동작합니다. 우리는 SA와 같은 휴리스틱 기법들을 사용하여 optimal point를 찾을 때에, 특정 initial point를 하나 잡아서 찾아나가는 것으로 항상 optimal solution을 찾는 것이 어려울 수 있습니다.
그렇기 때문에, 대부분의 경우, 여러가지 initial point를 잡고, 해당 지점들로부터 각각 SA를 적용시키면서 서로 다른 optimal point들을 찾은 후, 여러가지 시도들에서 찾은 가장 좋은 지점을 best solution으로 선택하는 방식으로 진행됩니다.
그러나 기존의 SA의 경우 다음과 같은 문제점이 있습니다.
만약 어떠한 initial point의 경우 최종까지 도달하더라도 5의 에너지를 가지고 있다고 합시다. 그러나 다른 initial point의 경우 3번의 step만에 1의 에너지를 가지게 되었습니다. 그러나 SA의 경우, 5의 에너지를 가진 것과 1의 에너지를 가진 point 모두 동일하게 계속해서 iteration을 거듭해가면서 solution을 찾으려 노력할 것입니다.
확률적으로는 중간 스텝에서도 높은 에너지를 갖는 포인트라면, 결과적으로도 best solution에 도달하지 못할 가능성이 높기 때문에, 낮은 에너지를 가지는 위치의 주변을 더 많이 살펴보는 것이 좋을 것이지만, 기존의 SA는 이를 고려하지 못합니다.
그렇기 때문에, 이러한 문제점을 해결하기 위해서 새로운 개념을 도입한 것이 바로 SMC-SA입니다.
SMC-SA의 경우 다음과 같이 동작합니다. 만약, 우리가 전체 K번의 iteration을 진행하며, 최대 N개의 서로 다른 initial point들에 대해서 SA를 시작한다고 합시다.
기존의 SA의 경우, 이들 N개의 포인트가 모두 서로 다르게 경로들을 찾으면서 내려갈 것입니다.
그러나 SMC-SA의 경우, 이들을 유기적으로 보기 위한 시도를 합니다.
각각의 initial point들에 대해서 하나씩 따로 iteration을 하는 것이 아닌, 전체 N개의 intial point들에 대해서 함께 iteration을 고려하는 과정을 진행합니다.
이 때, 각각의 point들이 갖는 self-normalized weights라는 새로운 개념을 도입합니다.
이 때, 각 point가 갖게 되는 weight는 다음과 같습니다.
- $w^{(n)}{k} = \frac{\pi{k}}{\pi_{k-1}}(x^{(n)}_{k-1})$, for $1 <= n <= N$
위와 같은 value를 갖게 되는 것은 결국 이전의 temperature에 대한 에너지 준위와 새로운 temperature에 대한 에너지 준위의 비를 통해서 weight가 결정되는 것입니다. 결국 이 과정에서도, 현재의 point가 가지는 에너지 준위가 낮을 수록 훨씬 더 높은 weight를 가지게 된다는 의미를 뜻합니다.
이를 통해서, 각각의 point가 가진 에너지에 따라서 이들이 가지는 weight들은 모두 다르게 됩니다.
이러한 상황에서, 우리는 k-th iteration에서 새롭게 G를 통해 neighbor point들을 생성하기 이전에, 이들을 생성할 후보군이 될 point들을 weight를 통해서 선정합니다. 즉, 높은 weight를 가진 수록, 후보로 선택될 가능성이 높으며, weight가 낮을수록 선택될 가능성은 낮아집니다.
이러한 과정을 Resampling이라고 합니다. 이러한 resampling을 통해서 어떠한 point는 여러번 선택될 수도, 어떠한 point는 선택되지 못할 수도 있습니다. 이 때에 선택되는 후보든 optimal에 가까운 점이 되고, 선택되지 못하는 후보는 optimal에서 멀 가능성이 높습니다. 물론 이 과정에서도 확률적으로 선택되지만, 기존에 모든 후보들이 동등한 기회를 가지던 상황과는 많이 다르게 흘러가게 된다는 것을 알 수 있습니다.
이렇게 새롭게 생성된 point들은 기존의 SA와 같이 볼츠만 분포에 따라서 새롭게 구한 확률에 따라서 다음 point로 선택될지, 혹은 선택되지 않을지 결정됩니다.
Convergence of SMC-SA
특정 포인트의 neighbor point를 생성하는 마르코브 커널 G가 ergodicity를 만족한다고 가정하고, $ℱ_{k}$가 k번의 iteration 동안 생성된 모든 샘플들의 히스토리라고 할 때, there exists a sequence ${c_{k}} \to 0$ s.t. for any bounded function $\phi$
-
$E[ μ_{k}(\phi) - π_{k}(\phi) ℱ_{k-1}] <= c_{k} \phi _{∞}$
위 식이 의미하는 바는, 주어지는 temperature decaying에 따라서, μ와 π가 점점 더 가까워지면서, 결국에는 최종적으로 도달하게 되는 후보지들이 optimal solution에 가까워진다는 것을 의미합니다. 기존의 SA에서 둘의 차의 limit가 0으로 수렴한다는 것을 의미하는 것처럼 converge할 수 있다는 것을 말합니다.
위의 식은 이론적으로 다음과 같은 c를 설정할 수 있을 때에 converge한다는 것을 보일 수 있으나 실질적으로 기존의 SA보다 더 낫다는 것을 이론적으로 보이기는 쉽지 않을 수도 있습니다.
그러나 많은 실험적 결과들이, 위와 같은 SMC-SA가 대다수의 경우 기존의 SA보다 낫다는 것을 emperical하게 보여줍니다.
SMC-SA example
Rosenbrock Function
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from ipywidgets import interactive
import random
import math
def rosenbrock(x, y, a = 1, b = 100):
return (a - x)**2 + b*((y - x**2)**2)
a = 1
b = 100
r = 0.1
bc = 10
T1 = 1
T2 = 1
seed = 2
max_iteration = 100
f = rosenbrock
random.seed(seed)
x1 = np.linspace(-2, 2)
x2 = np.linspace(-1, 3)
X1, X2 = np.meshgrid(x1, x2)
F = rosenbrock(X1, X2, a, b)
x = [-2.0, -1.0, 2.0, 3.0]
y = [-2.0, 2.0, -2.0, 2.0]
X = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
Y = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
best = [20000, 20000, 20000, 20000]
best_point = [(10, 10), (10, 10), (10, 10), (10, 10)]
def G(x, y, r):
a, b = random.uniform(-r, r), random.uniform(-r, r)
return x+a, y+b
def sa_p(E, bc, T):
return np.exp(-(E / (bc * T)))
def fsa_p(E, bc, T):
E = max(E, 0)
return 1 / (1 + (E / (bc * T)))
def plotter(E, A):
global X, Y
fig = plt.figure(figsize = [12, 8])
ax = plt.axes(projection='3d')
ax.plot_surface(X1, X2, F, cmap='jet', alpha=0.8)
ax.view_init(elev=E, azim=A)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('F(X, Y)')
for i in range(4): #SMC-SA
ax.scatter(X[max_iteration][2][i], Y[max_iteration][2][i], f(X[max_iteration][2][i], Y[max_iteration][2][i], a, b), color = 'dodgerblue')
for i in range(4):
for j in range(4):
X[0][i][j] = x[j]
Y[0][i][j] = y[j]
for k in range(max_iteration):
T1 = 1 / math.log(k+2)
T2 = 1 / ((k + 1) * math.log(k+2))
NX = [0, 0, 0, 0]
NY = [0, 0, 0, 0]
w = [0, 0, 0, 0]
#SMC-SA
if k > 0:
for j in range(4):
x, y = X[k-1][2][j], Y[k-1][2][j]
nx, ny = X[k][2][j], Y[k][2][j]
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
w[j] = sa_p(-fx, bc, T1) / sa_p(-fy, bc, T1)
sw = sum(w)
for i in range(4):
nowp = random.uniform(0, sw)
now = 0
for j in range(4):
now += w[j]
if(now >= nowp):
NX[i] = X[k][2][j]
NY[i] = Y[k][2][j]
break
for j in range(4):
X[k][2][j] = NX[j]
Y[k][2][j] = NY[j]
for j in range(4):
x, y = X[k][2][j], Y[k][2][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[2]:
best[2] = min(best[2], fy)
best_point[2] = (nx, ny)
p = sa_p(fy - fx, bc, T1)
now = random.uniform(0, 1)
if now < p:
X[k+1][2][j], Y[k+1][2][j] = nx, ny
else:
X[k+1][2][j], Y[k+1][2][j] = x, y
print('iteration %d - best score: %f / point (x, y) = (%f, %f)'%(k, best[2], best_point[2][0], best_point[2][1]))
print('\n\nlegend\n')
print('SMC SA - Dodgerblue points')
iplot = interactive(plotter, E = (-20, 90, 5), A = (-20, 90, 5))
iplot

Curious Simulated Annealing
Curious Simualted Annealing은 앞선 SA, FSA, SMC-SA에 대해 잘 이해하고 있다면 그리 어렵지 않은 방법론입니다. 그러나 그럼에도 불구하고, 앞선 알고리즘들의 장점을 흡수하여 굉장히 좋은 효율을 내는 알고리즘입니다.
기존의 FSA의 경우, SA가 가지고 있던, temperature decaying의 속도가 느리다는 점으로 인해, convergence speed가 느린 단점을 보완하고자 temperature 함수에 변형을 주는 것과 동시에, state의 probability를 결정하는 커널 함수를 변환시키는 식으로 동작했습니다.
그리고 SMC-SA의 경우, 기존의 방법들이 단일 point에 대한 simulated annealing의 단순 집합이라는 점을 해결하기 위해서, N개의 서로 다른 initial point들의 iteration을 모두 동시에 진행하면서, resampling이라는 기법을 도입해서 optimal solution에 도달할 확률이 높은 point가 잘 살아남을 수 있도록 만드는 기법을 도입했습니다.
이 둘을 합쳐서 CSA에서는 temperature function 및 probability kernel을 FSA에서 가져오고, 이 과정에서 iteration을 하는 때에 resampling을 진행하는 방법은 SMC-SA에서 가져와서 이 둘을 합친 방법으로 진행하게 됩니다.
그 결과, FSA가 가진 convergence speed가 빠르다는 장점과 SMC-SA가 가진 optimal solution에 도달할 가능성이 높은 후보들을 살린다는 장점이 결합되어 높은 성능을 보이게 됩니다.
Convergence of Curious SA
Curious SA의 convergence를 보장하는 것은 앞서 이야기한 FSA와 SMC-SA에서 이야기한 여러 조건들을 사용해서 보일 수 있습니다.
특정 포인트의 neighbor point를 생성하는 마르코브 커널 G가 ergodicity를 만족한다고 가정하고, $ℱ_{k}$가 k번의 iteration 동안 생성된 모든 샘플들의 히스토리라고 할 때, for any $\epsilon$, there exists $C_{\epsilon} > 0$ s.t.
-
$E[μ_{k}(S_{\epsilon}) ℱ_{k-1}] >= 1 - \frac{C_{\epsilon}}{(k+1)^{\gamma}}$
또한, ${x_{k}}가 CSA로부터 생성된 포인트 집합이라 할 때,
-
$E[μ_{k}(S_{\epsilon}) ℱ_{k-1}] >= P(x_{k})$
를 만족하기 때문에
- $P(x_{k}) >= 1 - \frac{C_{\epsilon}}{(k+1)^{\gamma}}$
즉, 결과적으로 위 식이 기존의 FSA의 결과와 동일해진다는 것을 알 수 있음, 이를 통해 우리는 CSA 또한 수많은 iteration 이후에는 결국에 convergence가 보장된다는 것을 알 수 있습니다.
CSA - example
Rosenbrock Function
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from ipywidgets import interactive
import random
import math
def rosenbrock(x, y, a = 1, b = 100):
return (a - x)**2 + b*((y - x**2)**2)
a = 1
b = 100
r = 0.1
bc = 10
T1 = 1
T2 = 1
seed = 2
max_iteration = 100
f = rosenbrock
random.seed(seed)
x1 = np.linspace(-2, 2)
x2 = np.linspace(-1, 3)
X1, X2 = np.meshgrid(x1, x2)
F = rosenbrock(X1, X2, a, b)
x = [-2.0, -1.0, 2.0, 3.0]
y = [-2.0, 2.0, -2.0, 2.0]
X = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
Y = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
best = [20000, 20000, 20000, 20000]
best_point = [(10, 10), (10, 10), (10, 10), (10, 10)]
def G(x, y, r):
a, b = random.uniform(-r, r), random.uniform(-r, r)
return x+a, y+b
def sa_p(E, bc, T):
return np.exp(-(E / (bc * T)))
def fsa_p(E, bc, T):
E = max(E, 0)
return 1 / (1 + (E / (bc * T)))
def plotter(E, A):
global X, Y
fig = plt.figure(figsize = [12, 8])
ax = plt.axes(projection='3d')
ax.plot_surface(X1, X2, F, cmap='jet', alpha=0.8)
ax.view_init(elev=E, azim=A)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('F(X, Y)')
for i in range(4): #CSA
ax.scatter(X[max_iteration][3][i], Y[max_iteration][3][i], f(X[max_iteration][3][i], Y[max_iteration][3][i], a, b), color = 'yellow')
for i in range(4):
for j in range(4):
X[0][i][j] = x[j]
Y[0][i][j] = y[j]
for k in range(max_iteration):
T1 = 1 / math.log(k+2)
T2 = 1 / ((k + 1) * math.log(k+2))
NX = [0, 0, 0, 0]
NY = [0, 0, 0, 0]
w = [0, 0, 0, 0]
# Curious SA
if k > 0:
for j in range(4):
x, y = X[k-1][3][j], Y[k-1][3][j]
nx, ny = X[k][3][j], Y[k][3][j]
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
w[j] = sa_p(-fx, bc, T1) / sa_p(-fy, bc, T1)
sw = sum(w)
for i in range(4):
nowp = random.uniform(0, sw)
now = 0
for j in range(4):
now += w[j]
if(now >= nowp):
NX[i] = X[k][3][j]
NY[i] = Y[k][3][j]
break
for j in range(4):
X[k][3][j] = NX[j]
Y[k][3][j] = NY[j]
for j in range(4):
x, y = X[k][3][j], Y[k][3][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[3]:
best[3] = min(best[3], fy)
best_point[3] = (nx, ny)
p = fsa_p(fy - fx, bc, T2)
now = random.uniform(0, 1)
if now < p:
X[k+1][3][j], Y[k+1][3][j] = nx, ny
else:
X[k+1][3][j], Y[k+1][3][j] = x, y
print('iteration %d - best score: %f / point (x, y) = (%f, %f)'%(k, best[3], best_point[3][0], best_point[3][1]))
print('\n\nlegend\n')
print('CSA - Yellow points')
iplot = interactive(plotter, E = (-20, 90, 5), A = (-20, 90, 5))
iplot
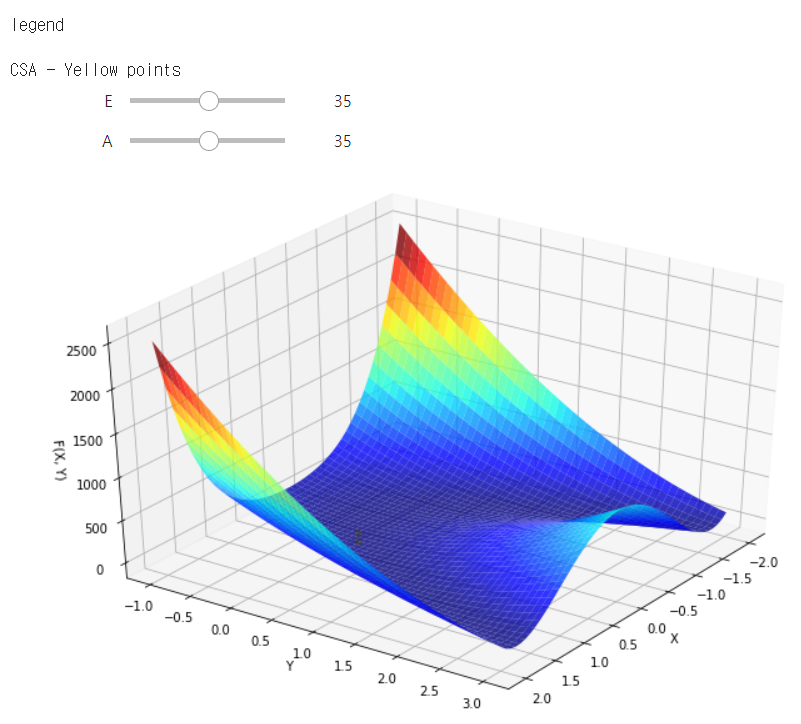
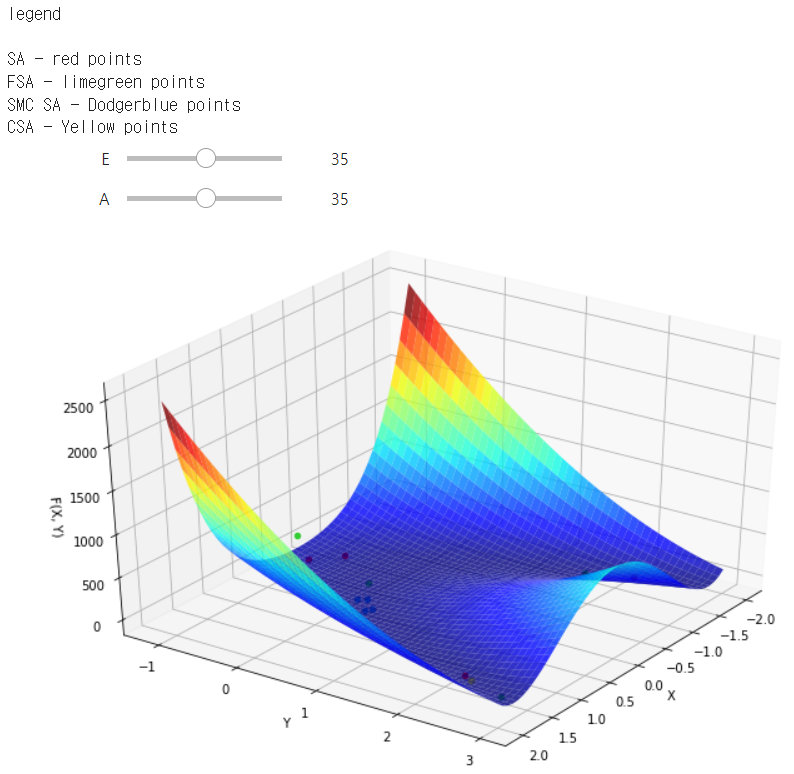
Simulated Annealing Example
여기에서는 앞서 이야기한 4가지의 모든 SA를 한 곳에 동작하여 결과를 확인합니다.
다만, 각각의 SA들은 특정 하이퍼파라미터에 따라서 결과가 굉장히 달라질 수 있고, 주어진 시작 지점, 사용한 마르코브 커널 G를 어떤 식으로 구현하는지에 따라서 다른 결과들을 내게 됩니다. 이에 관련된 튜닝은 직접 해보시면서 확인해보셔도 좋을 것 같습니다.
또한 SMC-SA와 CSA의 경우는, 기존 original SA와 FSA에는 없는 number of given initial points에 대해 영향을 크게 받기 때문에 결과를 살펴볼 때 유의가 필요합니다.
Rosenbrock Function
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from ipywidgets import interactive
import random
import math
def rosenbrock(x, y, a = 1, b = 100):
return (a - x)**2 + b*((y - x**2)**2)
a = 1
b = 100
r = 0.1
bc = 10
T1 = 1
T2 = 1
seed = 2
max_iteration = 100
f = rosenbrock
random.seed(seed)
x1 = np.linspace(-2, 2)
x2 = np.linspace(-1, 3)
X1, X2 = np.meshgrid(x1, x2)
F = rosenbrock(X1, X2, a, b)
x = [-2.0, -1.0, 2.0, 3.0]
y = [-2.0, 2.0, -2.0, 2.0]
X = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
Y = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
best = [20000, 20000, 20000, 20000]
best_point = [(10, 10), (10, 10), (10, 10), (10, 10)]
def G(x, y, r):
a, b = random.uniform(-r, r), random.uniform(-r, r)
return x+a, y+b
def sa_p(E, bc, T):
return np.exp(-(E / (bc * T)))
def fsa_p(E, bc, T):
E = max(E, 0)
return 1 / (1 + (E / (bc * T)))
def plotter(E, A):
global X, Y
fig = plt.figure(figsize = [12, 8])
ax = plt.axes(projection='3d')
ax.plot_surface(X1, X2, F, cmap='jet', alpha=0.8)
ax.view_init(elev=E, azim=A)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('F(X, Y)')
for i in range(4): #SA
ax.scatter(X[max_iteration][0][i], Y[max_iteration][0][i], f(X[max_iteration][0][i], Y[max_iteration][0][i], a, b), color = 'red')
for i in range(4): #FSA
ax.scatter(X[max_iteration][1][i], Y[max_iteration][1][i], f(X[max_iteration][1][i], Y[max_iteration][1][i], a, b), color = 'limegreen')
for i in range(4): #SMC-SA
ax.scatter(X[max_iteration][2][i], Y[max_iteration][2][i], f(X[max_iteration][2][i], Y[max_iteration][2][i], a, b), color = 'dodgerblue')
for i in range(4): #CSA
ax.scatter(X[max_iteration][3][i], Y[max_iteration][3][i], f(X[max_iteration][3][i], Y[max_iteration][3][i], a, b), color = 'yellow')
for i in range(4):
for j in range(4):
X[0][i][j] = x[j]
Y[0][i][j] = y[j]
for k in range(max_iteration):
T1 = 1 / math.log(k+2)
T2 = 1 / ((k + 1) * math.log(k+2))
for j in range(4): #SA
x, y = X[k][0][j], Y[k][0][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[0]:
best[0] = min(best[0], fy)
best_point[0] = (nx, ny)
p = sa_p(fy - fx, bc, T1)
now = random.uniform(0, 1)
if now < p:
X[k+1][0][j], Y[k+1][0][j] = nx, ny
else:
X[k+1][0][j], Y[k+1][0][j] = x, y
for j in range(4): #FSA
x, y = X[k][1][j], Y[k][1][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[1]:
best[1] = min(best[1], fy)
best_point[1] = (nx, ny)
p = fsa_p(fy - fx, bc, T2)
now = random.uniform(0, 1)
if now < p:
X[k+1][1][j], Y[k+1][1][j] = nx, ny
else:
X[k+1][1][j], Y[k+1][1][j] = x, y
NX = [0, 0, 0, 0]
NY = [0, 0, 0, 0]
w = [0, 0, 0, 0]
#SMC-SA
if k > 0:
for j in range(4):
x, y = X[k-1][2][j], Y[k-1][2][j]
nx, ny = X[k][2][j], Y[k][2][j]
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
w[j] = sa_p(-fx, bc, T1) / sa_p(-fy, bc, T1)
sw = sum(w)
for i in range(4):
nowp = random.uniform(0, sw)
now = 0
for j in range(4):
now += w[j]
if(now >= nowp):
NX[i] = X[k][2][j]
NY[i] = Y[k][2][j]
break
for j in range(4):
X[k][2][j] = NX[j]
Y[k][2][j] = NY[j]
for j in range(4):
x, y = X[k][2][j], Y[k][2][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[2]:
best[2] = min(best[2], fy)
best_point[2] = (nx, ny)
p = sa_p(fy - fx, bc, T1)
now = random.uniform(0, 1)
if now < p:
X[k+1][2][j], Y[k+1][2][j] = nx, ny
else:
X[k+1][2][j], Y[k+1][2][j] = x, y
# Curious SA
if k > 0:
for j in range(4):
x, y = X[k-1][3][j], Y[k-1][3][j]
nx, ny = X[k][3][j], Y[k][3][j]
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
w[j] = sa_p(-fx, bc, T1) / sa_p(-fy, bc, T1)
sw = sum(w)
for i in range(4):
nowp = random.uniform(0, sw)
now = 0
for j in range(4):
now += w[j]
if(now >= nowp):
NX[i] = X[k][3][j]
NY[i] = Y[k][3][j]
break
for j in range(4):
X[k][3][j] = NX[j]
Y[k][3][j] = NY[j]
for j in range(4):
x, y = X[k][3][j], Y[k][3][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[3]:
best[3] = min(best[3], fy)
best_point[3] = (nx, ny)
p = fsa_p(fy - fx, bc, T2)
now = random.uniform(0, 1)
if now < p:
X[k+1][3][j], Y[k+1][3][j] = nx, ny
else:
X[k+1][3][j], Y[k+1][3][j] = x, y
print('iteration %d - best score: %s / point (x, y) = (%s)'%(k, str(best), str(best_point[:])))
print('\n\n The result sequence is [SA, FSA, SMC-SA, CSA]')
print('\n\nlegend\n')
print('SA - red points')
print('FSA - limegreen points')
print('SMC SA - Dodgerblue points')
print('CSA - Yellow points')
iplot = interactive(plotter, E = (-20, 90, 5), A = (-20, 90, 5))
iplot
Result
SA - best score: 0.2700104447703194 / point (x, y) = (1.4847681534051314, 2.185825434596596)
FSA - best score: 0.46821023512643345 / point (x, y) = (1.6705793344001245, 2.804449125878089)
SMCSA - best score: 0.15545297338207104 / point (x, y) = (0.6769967144545007, 0.4357144096513451)
CSA - best score: 0.2516899318566773 / point (x, y) = (1.4993199325898567, 2.2528280490561143)
마치며
이 post에서는 derivative-free optimization problem에서 최적화하기 위한 휴리스틱 기법인 Simulated Annealing에 대해 다루었습니다. 가장 기본적인 형태의 SA부터, 이를 최적화하기 위해 나온 여러가지 아이디어들인 FSA, SMC-SA, 그리고 가장 최근에 발표된 Curious SA까지, SA 기법을 최적화하기 위해 어떠한 방식의 접근 방법들이 있었는지에 대해 이야기하며, 각각의 기법들이 실제 해로 도달할 수 있는지에 대한 convergency에 대해서도 다루었습니다.
이러한 형태의 SA들은 위에서 언급한 함수들 이외에도 굉장히 다양한 형태의 optimization을 해결하는데 큰 도움을 줍니다. 또한 함수 자체의 연속성 등에 대해서도 보장이 되지 않더라도 적용할 수 있다는 장점이 있으며, 기본적으로 어려운 문제인 black box 상황에서도 최적의 결과를 낼 수 있도록 접근하는 방법론을 알려준다는 점에서 큰 의의가 있습니다.
해당 글을 통해서 여러가지 최적화 기법들에 대한 관심을 갖고, 그 중에서도 여러가지에 적용이 가능한 메타 휴리스틱 기법인 simulated annealing에 대한 많은 정보를 얻어갈 수 있었으면 좋겠습니다.
Related Paper
2. D. Bertsimas, et al. Simulated annealing. Statistical Science, 1993.
4. H. Szu, R. Hartley. Fast simulated annealing, Physics Letters A, 1987.