variational quantum algorithm

quantum , variational-quantum-circuit , variational-quantum-eigensolver , vqa , vqc , vqe

서론

Keywords: VQC(Variational Quantum Circuit), VQA(Variational Quantum Algorithm), VQE(Variational Quantum Eigensolver), Observable, Hamiltonian

기본적인 양자상태의 표현과 gate가 어떻게 작동하는지는 이해하고 있다는 가정하에 글을 작성하였다.

VQC, VQA, VQE 모두 양자 컴퓨팅에서 중요한 개념들이지만 한국어로 제대로 소개된 글이 없기에 이 글을 통해 소개하고자 한다

Quantum Circuit

그림 1. 양자회로의 모습

위 그림 1은 일반적인 양자회로의 모습을 나타내고 있다. 고전 회로에서 1-input gate인 Inverter과 2-input gate인 AND, OR, XOR게이트, 3-input gate인 3-input OR 등등이 있듯이 양자 회로에도 다양한 개수의 입력을 받는 회로가 있다.

양자 회로를 나타낸 그림 1에서는 1-input gate인 H, X gate와 2-input gate인 CNOT(Controlled-Not)게이트를 확인할 수 있다. 이 게이트들은 각각 고정된 역할을 맡으며 파라미터에 의해 조정되지 않는다.

Variational Quantum Circuit(VQC) 또는 Parameterized Quantum Cirquit(PQC)

그림 2. 파라미터에 의해 조정되는 양자 회로의 모습

하지만 위 그림 2와 같은 회로는 RX(rotate x), RY(rotate y), RZ(rotate z) 게이트가 사용되었고, 이 게이트들은 회전 게이트로써 얼마나 회전 시킬지에 대한 정보를 파라미터로 받는다. 잘 보면 그림 2의 아래쪽에 써져 있는 값들을 볼 수 있는데 저 값이 파라미터이다. 예를 들어, RX(0.3) 은 0.3만큼 X축으로 회전시키는 게이트이다.

우리가 파라미터들을 가지고 있고, 이 값을 조정한다면 회로의 출력 또한 자연히 바뀔 것이다. 이러한 회로를 Variational Quantum Circuit이라고 한다.

Variational Quantum Algorithm(VQA)

양자 컴퓨팅 세계에서 관측 가능한 모든 값들은 Observable로 표현된다. 예를 들어, 운동량을 나타내는 Observable, 또는 에너지를 나타내는 Observable, 단순히 별 의미 없는 특성을 나타내는 Observable 등등이 있다.

그럼 파라미터들로 조정되는 회로를 구성한 뒤, Observable의 값을 측정하는 회로를 생각해 보자. 파라미터의 값이 바뀔수록 당연히 Observable의 기댓값도 바뀔 것이다.

그림 3. VQA의 대략적인 모습

파라미터의 값이 바뀔 때 Observable의 기댓값이 바뀐다면 이를 최소화하는 파라미터를 찾는 것이 가능하지 않을까 하는 생각이 든다. 이 아이디어에서 출발한 것이 Variational Quantum Algorithm(VQA)이다.

더 구체적으로는, 고전적으로 회로를 시뮬레이션 할 때는 계산과정을 전부 알고 있으므로 머신러닝에서 gradient를 계산하는것과 같은 방법으로 최적화가 가능하다. 머신러닝과 거의 유사하다. Optimizer도 Adap optimizer 등등을 사용한다.

만약 실제 양자컴퓨터를 사용한다면 이 방법이 불가능할까? 다행히도 parameter shift rule이라는 좋은 방법이 존재한다. 양자컴퓨터에서 내부적으로 얽힘을 사용한 복잡한 계산을 하여도, 그 계산과정을 따라갈 수 없는데도 parameter의 gradient를 구할 수 있게 해주는 방법이다. 이것도 한국어로 제대로 소개된 글이 없으니 다음에 소개하도록 하겠다.

여튼, 파라미터를 바꿔가며 Observable을 cost function으로 생각했을때 최소값을 찾는 것이 가능하다. 이것이 Variational Quantum Algorithm이다.

Variatonal Quantum Eigensolver(VQE)

VQE는 VQA의 특수한 집합이다. VQA는 파라미터 조정을 통한 최적화가 가능한 모든 문제에 적용 가능한데, VQE는 이름에서 알 수 있듯이 주어진 Observable의 eigenvector을 찾는 알고리즘이다.

갑자기 왜 observable의 고유벡터가 튀어나올까? 이건 Observable의 성질과 관련 있다. Observable의 관측값은 Observable의 고유값의 조합이다. 임의 상태 벡터를 Observable의 고유벡터들의 선형 결합으로 표현되었을때, 그 확률에 비례하여 고윳값 중에 하나가 관측된다. 따라서 Observable의 평균값은 고유값의 조합이 된다.

이제 Observable의 관측값을 최소화하는 VQA를 생각해 보자. 모든 관측값은 Observable의 고윳값들에 확률벡터를 내적한 값이므로 관측값이 최소가 된다는 것은 Observable의 최소 고유값이 된다는 듯이다. 이때의 상태는 당연히 Observable의 최소 고유값에 대응되는 고유벡터가 된다. 이 알고리즘이 Variational Quantum Eigensolver라고 불리는 이유가 여기에 있다.

Hamiltonian

이제 Hamiltonian을 생각하자. Hamiltonian는 Observable의 일종으로, 대응되는 값이 에너지일때 그 Observable을 hamiltonian이라고 부른다.

다시 앞의 VQE를 떠올려 보자. VQE에서 hamiltonian의 최소 관측값을 찾았다는 것은 hamiltonian의 최소 고유값을 찾았다는 것이다. 그런데 Hamiltonian의 최소 고윳값은 정의에 의해 계가 취할 수 있는 여러 에너지 준위들 중 최소값이라는 의미이다.

즉, VQE를 사용하여 Hamiltonian의 최소 고유값을 찾는 것은 계의 바닥상태 에너지를 찾는 것과 같다.

VQE의 응용 - Quantum chemistry

배경 설명

이제 VQE의 가장 간단한 응용인 오비탈의 바닥상태에서 전자배치를 찾는 문제를 풀어 보자. 이 문제가 좀 더 복잡한 이유는, 양자역학적으로 중첩된 상태가 바닥상태가 될 수 있다는 점이다. 즉, s와 p오비탈에 전자를 두개 배치하는 경우를 떠올려보자. 일반적으로 바닥상태는 당연히 s오비탈에 스핀 업, 다운으로 전자 두개를 배치하는 경우이다. 그러나 중첩을 고려한다면

90%확률로 s오비탈에 전자 두개, 10%확률로 s오비탈, p오비탈에 전자 하나씩

이 배치가 좀 더 에너지가 낮을 수도 있는데, 이는 굉장히 신기한 일이다. 일반적으로 s오비탈에 전자가 전부 배치되는것이 제일 에너지가 낮을 것이라 생각하지만 중첩을 고려한다면 여러 배치가 중첩된 상태가 에너지가 더 낮을 수도 있다.

이를 고려하려면 당연히 고전적인 계산보다는 양자컴퓨팅을 사용한 계산이 자연스러울 것이다. 따라서 양자 컴퓨팅을 사용한 해결방법을 다뤄 보자. 간편하게 VQE를 코딩할 수 있는 pennylane 을 사용하여 설명할 것이다.

VQE를 사용한 해결 - 개요

VQE를 사용하여 대부분의 문제를 해결하는 방법은 아래와 같이 요약할 수 있다.

문제를 파악하고, 어떻게 상태를 양자 상태에 인코딩하여 표현할지 결정한다.
인코딩을 바탕으로 그 계의 에너지를 설명할 Hamiltonian을 구성한다.
VQE를 사용하여 그 Hamiltonian의 최소 고유값을 찾는다.
구한 최소 고윳값이 계의 최소 에너지이고, 그때의 상태가 계의 바닥상태이다.

1. 양자 상태 인코딩

양자컴퓨터를 사용하여 문제를 해결하려면 상태를 어떻게 큐비트로 표현할지를 정해야 한다. 이 문제에서는 second quantization를 사용할 것이다. second quantization은 양자상태에서 해당 상태의 몇개의 입자가 있는지를 표현할 때 쓰이는 방식이다. 예를 들어 상태 A에 입자가 2개, 상태 B에 전자가 3개라고 하면 아래와 같이 표현한다.

\[\vert 2_A\rangle \otimes \vert 3_B\rangle\]

하지만 이 글에서 이 내용을 자세히 다루기는 어려우니 단순하게 큐비트를 사용하여 각 상태별로 입자의 개수를 나타내는 인코딩 방식이라고 생각하면 된다.

우리는 오비탈에 전자를 배치하는 문제를 풀 것이므로 아래와 같은 오비탈을 생각해 보자.

그림 4. H2 분자의 혼성 오비탈

전자를 배치 가능한 오비탈은 2개이고 스핀은 두개가 가능하므로 총 전자가 취할 수 있는 상태는 4개이다. 이를 4큐빗으로 표현하고, 큐비트가 배치되면 1 배치되지 않으면 0으로 표현할 수 있다.

\[\vert 1100\rangle\]

위 상태의 큐비트는 4개이고 1은 2개이다. 이 상태는 위 그림 4의 상태에 대응된다. 첫 두개의 큐비트는 첫 오비탈의 업 스핀, 다운 스핀 상태의 점유 여부를 말한다. 1이면 그 상태가 점유된 것이고 0이면 점유되지 않은 것이다.

따라서 오비탈이 N개라면 큐빗은 2N개가 필요하단 걸 유추할 수 있다. 또한 1의 개수가 배치할 전자의 개수가 된다. 큐비트는 0 또는 1이므로 같은 오비탈, 같은 스핀을 가진 전자가 2개 이상 존재할 수 없다는 조건도 자연스럽게 만족한다.

이제 N큐빗에 e개의 전자를 배치하는 문제에서 고전적인 바닥상태는 2N개의 큐빗을 왼쪽부터 e개만 1을 채우는 상태일 것이다. 이 상태를 hartree-fock state라고 하며, 중첩을 고려한 바닥상태 에너지의 상한값이다. 중첩을 고려하면 최소한 hf state보단 에너지가 줄어들기 때문이다.

예를 들어, 오비탈 10개의 전자 14개를 배치하는 상황의 hf state는 $\vert 11111111111111000000\rangle$ 이다.

2. Hamiltonian 구성

Hamiltonian은 오비탈 간 전자들, 오비탈 자체의 에너지를 종합적으로 고려하여 계산된다. Hamiltonian계산에 대한 내용은 링크를 참고하면 된다. 굉장히 복잡한 계산식을 거치지만, pennylane을 사용하면 쉽게 계산할 수 있으니 넘어가자. 아래 코드를 작성하면 H2분자의 Hamiltonian을 구할 수 있다.

import pennylane as qml
from pennylane import qchem
from pennylane import numpy as np

symbols = ["H", "H"]
coordinates = np.array([0.0, 0.0, -0.6614, 0.0, 0.0, 0.6614])
basis_set = "sto-3g"
electrons = 2

H, qubits = qchem.molecular_hamiltonian(
    symbols,
    coordinates,
    basis=basis_set,
)
print("Hamiltonian is\n\n", H)
print("Number of qubits: ", qubits)

위 코드에서 coordinates는 두개의 수소원자의 3차원 공간 좌표이다. 둘 사이의 좌표 차이가 대략 1.32정도 나는데, 이건 실제 수소분자의 원자핵간 거리를 bohr radius단위로 나타낸 값이다.

ansatz구성

Hamiltonian을 구했으니, 이제 파라미터에 의해 조정되는 회로를 만들자. 파라미터에 의해 조정되는 회로를 ansatz라고 한다. 딥러닝에서 신경망의 종류가 많듯이 VQA에서 ansatz의 종류 또한 굉장히 많다. 목적에 따라 적절한 ansatz를 구성해야 훨씬 빠르고 정확하게 정답을 찾을 수 있어 굉장히 중요한 문제이다. 신경망의 종류가 주는 영향을 생각하면 된다.

문제마다 적절한 ansatz설계하는 것은 고민해봐야할 문제이지만, 이 경우에는 pennylane에서 제공하는 간단한 코드를 사용하면 된다.

그림 5. qml.AllSinglesDoubles

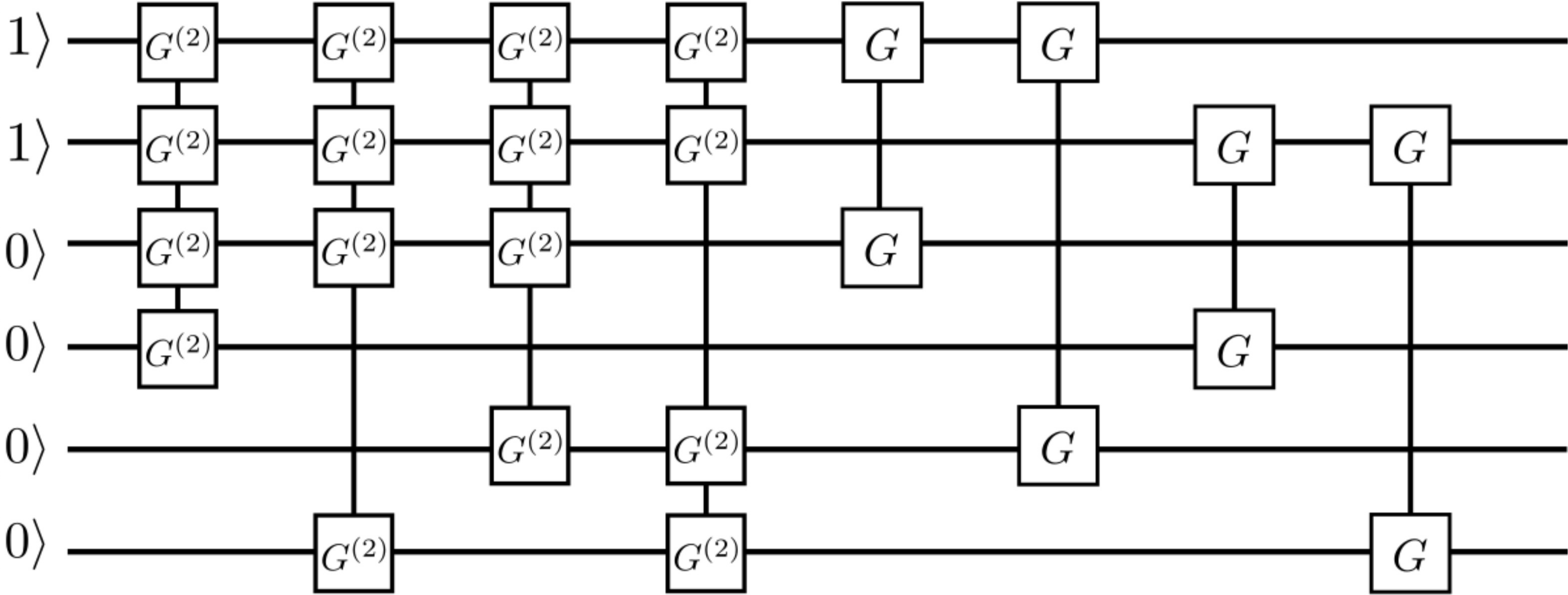
이 ansatz는 전자의 모든 들뜸을 볼 수 있도록 설계되었다. 위 그림 5에서 앞선 게이트 4개는 DoubleExcitation이고 뒤의 게이트 4개는 SingleExcitatioin이다. 이를 통해 큐빗 6개, 전자 2개가 점유된 hf state에서 모든 들뜸을 고려할 수 있다.

따라서 파라미터를 잘 조정하면 $\vert 1100\rangle$이 $\vert 0011\rangle$ 이 될 수도 있고, $\vert 0110\rangle$ 이 될 수도 있다. 여러 상태들의 중첩도 가능하다. 중요한 점은 현재 문제에서는 1의 개수가 전자의 개수를 의미하기 때문에 ansatz또한 1의 개수를 보존해야 한다는 점이다. 이를 U(1) symmetry라고 하는데, 위의 Single Excitation과 Double Excitation은 전자의 들뜸만 고려하기 때문에 1의 개수(전자의 개수)를 보존한다.

cost function 구성

cost function은 정말 간단하다.

@qml.qnode(dev, interface="autograd")
def cost_fn(theta):
    circuit_VQE(theta, range(qubits))
    return qml.expval(H)

단순히 앞에서 구한 수소분자 Hamiltonian의 기댓값을 구하는 코드이다.

최적화

# 최적화 세팅
stepsize = 0.01
max_iterations = 100
opt = qml.AdamOptimizer(stepsize=stepsize)
theta = np.zeros(num_theta, requires_grad=True)

# 최적화 진행
theta_opt = None
energy_VQE = 1e5
energy = []
params = []

for n in range(max_iterations):
    params.append(theta)
    theta, prev_energy = opt.step_and_cost(cost_fn, theta)
    energy.append(prev_energy)
    sample = cost_fn(theta)
    if sample < energy_VQE:
        energy_opt = sample
        theta_opt = theta

print("Final VQE energy: %.4f" % (energy_VQE))
print("Optimal parameters:", theta_opt)

최적화는 AdamOptimizer를 사용했다. 파라미터를 나타내는 변수가 theta인데 0으로 초기화되어 있다. theta가 0일때 hf state이고 theta를 바꿔감에 따라 결과가 바뀐다. 나중에 최적화 그래프에서 초기값이 hf state의 energy라고 생각하면 된다. 최적화를 진행해나가면서 우리는 hf state보다 더 안정된 “중첩된”상태를 발견할 것이다.

최적화 결과

그림 6. 최적화 결과

처음에 Hf state의 에너지부터 시작해서 좀 더 에너지가 낮아졌다. 큰 차이는 아니지만 오비탈의 바닥상태부터 전자를 가득 채운 상태보다 더 낮은 에너지가 존재한다는 것을 확인할 수 있었다.

실제로 조사해보면 $\vert 1100\rangle$ 상태가 98.9%, $\vert 0011\rangle$상태가 1.1%였다. 낮긴 하지만 들뜬 상태가 조금 중첩되어 있었다.

이 글은 페니레인 문서 를 참고하여 작성된 글이다. 더 궁금한 내용이 있다면 이 글을 참고하길 바란다.

결론

양자컴퓨팅을 사용하여 수소분자의 전자가 어떻게 배치되어 있는지를 조사할 수 있었다. 전자가 어느 한 오비탈에 고정적으로 배치되어 있지 않고, 여러 오비탈에 중첩되어 있음을 확인할 수 있었다.

이외에도 VQA의 활용방안은 굉장히 많으니 흥미가 생긴다면 더 찾아보길 바란다.

참고문헌

[1] https://docs.pennylane.ai/en/stable/introduction/chemistry.html

[2] https://docs.pennylane.ai/en/stable/code/api/pennylane.AllSinglesDoubles.html