Polya's Enumeration Theorem을 이용한 카운팅 문제 해결
개요
Polya’s Enumeration Theorem(포여 열거 정리)는 어떤 작용에 대한 equivalence class의 개수를 구할 때 사용됩니다. 대표적인 예시로 돌리거나 뒤집어서 같은 것을 하나로 볼 때, 서로 다른 목걸이의 개수를 구하는 문제가 있습니다.
이 글에서는 Burnside Lemma와 그것의 일반화인 Polya’s Enumeration Theorem을 소개한 후 이를 적용하여 문제를 해결하는 과정을 서술하겠습니다.
관련 문제는 백준 문제집 또는 알고리즘 분류에서 찾아볼 수 있습니다. 해당 태그를 가진 문제가 9문제에 불과한 만큼 CP에서 자주 등장하는 주제는 아닙니다. 그렇지만 특정 형태의 카운팅 문제를 크게 단순화해주는 도구입니다.
Burnside Lemma(번사이드 보조정리)
$G$는 유한한 집합 $X$에 작용하는 유한한 Group입니다. $r$을 궤도의 개수라고 하면 다음이 성립합니다. \(r=\frac{1}{\vert G\vert}\sum_{g\in G}\vert X_g\vert\)
$x_1, x_2\in X$에 대해 $gx_1=x_2$를 만족하는 $g\in G$가 있을 때 $x_1$과 $x_2$를 equivalent하다고 하면, $X$를 equivalent한 원소들끼리 묶을 수 있습니다. 이때 각 묶음을 “궤도”라고 합니다. 그리고 $X_g$는 $gx=x$를 만족하는 $x$들의 집합입니다.
이를 문제 상황에 대응해 보겠습니다. 정사각형의 4개의 꼭짓점을 흰색이나 검은색으로 칠할 때, 꼭짓점에 번호를 붙여 색칠한 방법들을 집합 $X$에, 정사각형을 돌리거나 뒤집는 것을 Group $G$에, 돌리거나 뒤집어서 같아지는 정사각형들의 묶음을 궤도에 대응할 수 있습니다.
$G$의 원소들을 permutation으로 나타내면 다음과 같습니다 : $g_0=id$, $g_1=(1234)$, $g_2=(13)(24)$, $g_3=(1432)$, $g_4=(12)(34)$, $g_5=(14)(23)$, $g_6=(13)$, $g_7=(24)$
각 permutation을 적용해도 색의 배치가 변하지 않는 것들의 집합이 $X_g$입니다. 각 $g_i$에 대한 $\vert X_g\vert$는 각각 16, 2, 4, 2, 4, 4, 8, 8입니다. 이를 위의 식에 대입하면 $r=\frac 18(16+2+4+2+4+4+8+8)=\frac{48}{8}=6$입니다. 그림으로 서로 다른 색칠이 6개임을 확인할 수 있습니다.
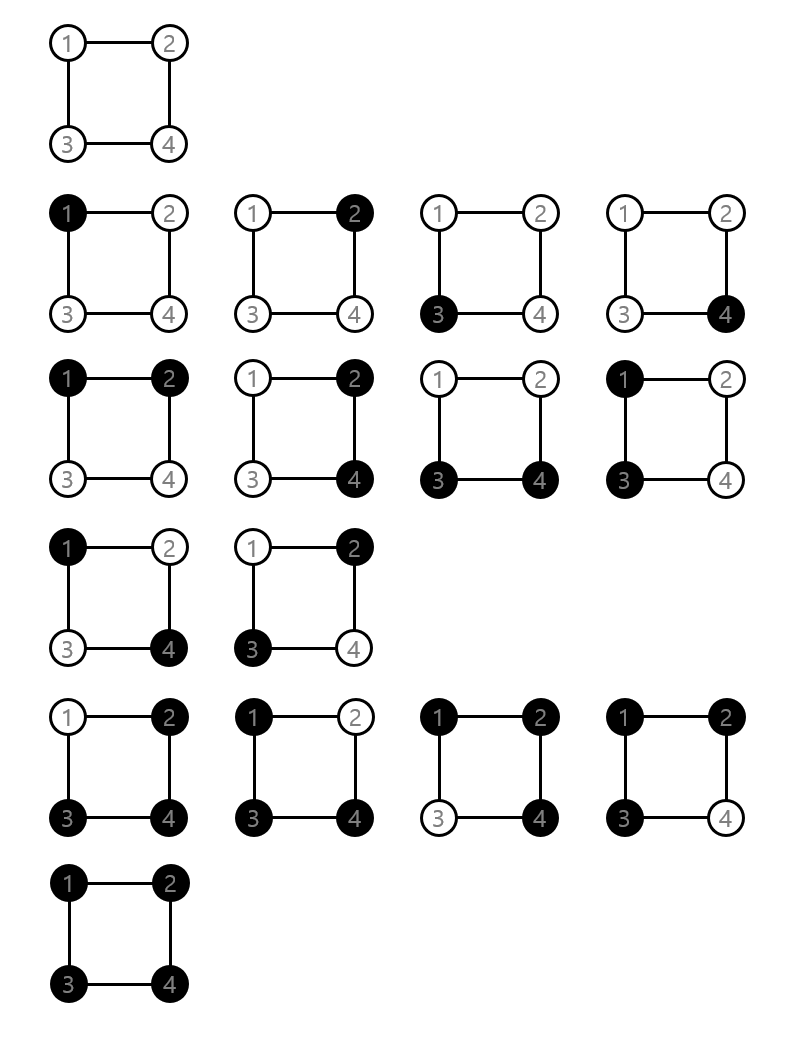
Polya’s Enumeration Theorem(포여 열거 정리)
$G$의 cycle index를 ${a_1}^{j_1(g)}{a_2}^{j_2(g)}{a_3}^{j_3(g)}\cdots$의 평균으로 정의합니다. 이때 $j_k(g)$는 $g$를 disjoint한 사이클로 분해했을 때 길이 $k$인 사이클의 개수입니다. $G$의 cycle index $Z(G)$는 다음과 같습니다. \(Z(G)=\frac{1}{\vert G\vert}\sum_{g\in G}\prod_{k=1}^{n}{a_k}^{j_k(g)}\)
이를 바탕으로 서로 다른 색칠의 개수를 색 $c_1, c_2, \cdots, c_m$이 칠해진 횟수에 따라 구할 수 있습니다. $a_i={c_1}^i+{c_2}^i+\cdots+{c_m}^i$로 치환하면
\[K_E(c_1, c_2, \cdots, c_m)=\frac{1}{\vert G\vert}\sum_{g\in G}\prod_{k=1}^{n}{({c_1}^k+{c_2}^k+\cdots+{c_m}^k)}^{j_k(g)}\]입니다. $K_E$는 각 색을 변수로 갖는 생성함수로, ${c_1}^{b_1}{c_2}^{b_2}\cdots{c_m}^{b_m}$의 계수는 $1\leq i\leq m$에 대해 $c_i$가 $b_i$번 사용된 서로 다른 색칠의 개수를 의미합니다.
$c_1, c_2, \cdots, c_m$에 모두 1을 대입하면 번사이드 보조정리와 같은 결과를 얻을 수 있습니다.
위의 예시에서 $G$의 원소들의 cycle index는 다음과 같습니다 : $g_0={a_1}^4$, $g_1=a_4$, $g_2={a_2}^2$, $g_3=a_4$, $g_4={a_2}^2$, $g_5={a_2}^2$, $g_6={a_1}^2a_2$, $g_7={a_1}^2a_2$
이를 모두 더하고 평균을 내면 $Z(G)=\frac 18({a_1}^4+2{a_1}^2a_2+3{a_2}^2+2a_4)$입니다. $a_1=b+w, a_2=b^2+w^2, a_4=b^4+w^4$로 치환 후 식을 정리하면 $K_E(b, w)=b^4+b^3w+2b^2w^2+bw^3+w^4$로 위의 그림에서 확인할 수 있는 결과가 나옵니다.
연습문제
번사이드 보조정리, 포여 열거 정리는 “$A$해서 같아지면 같다고 가정할 때, 서로 다른 $B$의 개수를 구하시오” 형태의 문제를 풀 때 쓰일 수 있습니다. 우선 $A$를 $G$에, $B$를 $X$에 대응한 다음, 필요하다면 $G$가 Group이 되도록 확장하여 재정의합니다. 다음으로 $B$ 중에 $A$하더라도 변하지 않는 것의 개수($\vert X_g\vert$)를 구합니다. 이를 모든 $A$에 대해 반복하여 합한 뒤, $A$의 개수로 나누면 됩니다. 이런 방법을 바탕으로 다음 문제들을 풀어보겠습니다.
문제 1: Educational Codeforces Round 52 E. Side Transmutations
요약
문자 집합 $A$로 이루어진 길이 $n$의 문자열 $\vert A\vert^n$개가 있습니다. 그리고 $1\leq i \leq m$인 $i$에 대해 길이 $b_i$의 prefix와 suffix를 떼어서 뒤집은 다음에 각각 반대쪽에 다시 붙이는 move가 있습니다. 예를 들어서 “abcdefghi”에 $b_1$에 대한 move를 적용하면 “ihcdefgba“가 됩니다. $m$가지의 move를 통해 $S$에서 $T$를 만들 수 있다면 $S$와 $T$가 같다고 가정합니다. 이때, 서로 다른 문자열의 개수를 $998244353$으로 나눈 나머지를 구하는 문제입니다.
풀이
문자열의 집합을 $X$, move의 집합을 $G$라 하면, 문자열에 move를 적용하는 것은 $X$ 위에서 $G$의 Group Action이라고 볼 수 있습니다. 우선 문제에서 주어진 move들로만 $G$를 구성했을 때, 이것이 Group이 되는지를 확인해야 합니다.
예를 들어 $b_1=2$, $b_2=4$에 대한 move를 각각 $g_1, g_2 \in G$라 하겠습니다. 이 move를 “abcdefghi”$=x\in X$에 적용하면 $g_1x=$”ihcdefgba”, $g_2x=$”ihgfedcba” 입니다.
Group Action의 정의에 의해, $(g_1g_2)x=g_1(g_2x)$를 만족해야 합니다. $g_2x$의 결과 “ihgfedcba”에 $g_1$을 적용하면 “abgfedchi”로, 앞뒤에서 3~4번째 문자가 뒤집힌 형태입니다. 그러나 문제에서 주어진 move들로는 prefix와 suffix가 아닌 문자열의 중간 부분을 뒤집을 수 없습니다. $G$는 문제에서 주어진 move들로만 포함하기 때문에 $g_1g_2$는 $G$에 포함되지 않고, Group의 조건에 위배됩니다.
그러므로 이 문제를 해결하기 위해 $G$를 확장하여 다시 정의해야 합니다. $G$를 길이 $m$인 $2^m$개의 binary string 들의 집합으로, $g_1, g_2\in G$에 대해 $g_1g_2$를 $g_1$과 $g_2$ 의 XOR 연산으로 정의합니다. 그리고 $g \in G$, $x \in X$에 대해 $gx$를 $g$의 $i$번째 bit가 1이라면 $b_{i-1} \lt j \leq b_i (b_0=0)$에 대해 $x$의 앞에서 $j$번 문자와 뒤에서 $j$번 문자를 swap하는 것으로 정의합니다.
예를 들어 $b_1=2$, $b_2=4$, $b_3=7$이고 $x=$”abcdefghijklmnopqrst”, $g=101$이라면 $gx$는 다음과 같습니다.
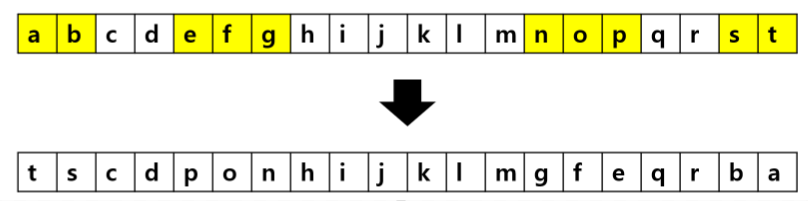
이제 모든 $g \in G$에 대해 $gx=x$를 만족하는 $x$의 개수를 계산해 봅시다. $gx=x$를 만족하기 위해서는 $g$에서 swap하게 되는 모든 인덱스 쌍$(i_1, i_2)$에 대해 $i_1$번째와 $i_2$번째 문자가 같으면 됩니다. 그런 쌍이 총 $q$개라면 $gx=x$를 만족하는 $x$의 개수는 $\vert A\vert^{n-q}$입니다. 그리고 $q$는 $i$번째 bit가 1인 $i$에 대해 $b_i-b_{i-1}$을 모두 합한 것입니다.
모든 $g \in G$에 대해 $\vert A\vert^{n-q}$의 합을 구한 뒤 $\vert G\vert=2^m$으로 나누면 이 문제의 답을 얻을 수 있습니다. 1번부터 $i$번 비트까지의 길이 $i$의 binary string $2^i$개에 대한 $\sum\vert A\vert^{n-q}$를 $S_i$라고 합시다. 여기에 $i+1$번째 비트를 추가할 때, $i+1$번째 비트가 0과 1인 $2^i$개의 binary string에 대한 $\sum\vert A\vert^{n-q}$는 각각 $S_i$, $\frac{S_i}{\vert A\vert^{b_{i+1}-b_i}}$입니다. 1인 비트가 추가됨으로 각각의 binary string에 대해 $q$가 $b_{i+1}-b_i$만큼 증가했기 때문입니다. 즉 $S_{i+1}=S_i+\frac{S_i}{\vert A\vert^{b_{i+1}-b_i}}$입니다. $S_0=\vert A\vert^n$부터 시작하여 $S_m=\sum_{g \in G}\vert A\vert^{n-q} $을 $O(m)$ 시간에 계산할 수 있습니다.
문제 2: BOJ #18567. Kaleidoscope
요약
정12면체의 각 면을 5등분한 형태의 60면체의 면을 $n$가지 색으로 칠하되 $i$번째 색은 최소 $c_i$번 사용하여야 합니다. 돌렸을 때 색의 배치가 같다면 같은 색칠로 간주할 때, 서로 다른 색칠의 수를 구하는 문제입니다.
풀이
각 면을 색칠하는 방법을 $X$, 60면체를 돌리는 것을 $G$라 하면, 색칠된 60면체를 돌리는 것을 $X$ 위에서 $G$의 Group Action으로 볼 수 있습니다. 60면체의 대칭축은 다음과 같습니다.
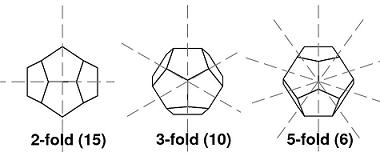
정12면체에는 꼭짓점, 모서리, 면을 중심으로 각각 10, 15, 6개의 축이 있습니다. 꼭짓점 축에는 3개의 면이 모여 있고 $120^\circ$, $240^\circ$ 돌렸을 때 각 면들이 돌리기 전 다른 면들의 위치에 오게 됩니다. 따라서 꼭짓점 축을 중심으로 회전하는 방법은 2가지가 있습니다. 마찬가지로 모서리 축에는 2개의 면이 모여 있고 $180^\circ$만큼 돌릴 수 있으며 회전하는 방법은 1가지가 있습니다. 마지막으로 면 축에는 5개의 면이 모여 있고 $72^\circ$, $144^\circ$, $216^\circ$, $288^\circ$만큼 돌릴 수 있으며 회전하는 방법은 4가지가 있습니다.
여기에 어느 축으로도 회전하지 않는 방법도 있으므로 1가지를 더하면 $G$에는 $10\times 2+15\times 1+6\times 4+1=60$개의 원소가 있습니다.
각각의 $g \in G$에 대해 $gx=x$를 만족하는 $x$의 개수를 계산해 봅시다. 각 종류의 축에 대해서 이를 계산한 다음 모두 더하면 됩니다. 먼저 꼭짓점 축부터 보겠습니다. 돌리기 전후의 면을 대응한 다음 사이클로 분할하면 길이 3의 사이클 20개로 분할됩니다. 그리고 $gx=x$를 만족하기 위해서 각 사이클에 속한 면들을 모두 같은 색으로 칠해야 합니다. $dp(i, j)$를 $1$번 색부터 $i$번 색까지 문제의 조건을 만족하면서 사용했을 때, 지금까지 $3\times j$개의 면을 색칠하는 방법의 수로 정의합니다. 그렇다면 다음과 같은 점화식을 세울 수 있습니다. $i-1$개의 색으로 칠하는 방법의 수와, 아직 칠해지지 않은 면을 $i$번 색으로 칠하는 방법의 수의 곱을 모두 더하는 방식입니다.
\[dp(i, j)=\sum_{\lceil \frac{c_i}{3} \rceil \leq k \leq j}dp(i-1, j-k)\times {20-j+k \choose k}\]$dp(0, 0)=1$부터 시작하여 $dp(n, 20)$까지 계산합니다. 여기에 꼭짓점 축으로 돌릴 때의 $g$의 개수 $20$을 곱하면 됩니다. 60면체의 면의 개수를 $F=60$이라 하면 시간복잡도는 $O(F^2n)$입니다. 모서리, 면 축으로 회전할 때와 회전하지 않을 때도 비슷한 방법으로 계산해서 모두 더하면 됩니다.
더한 결과를 $\vert G\vert=60$으로 나누면 이 문제의 답이 됩니다. 문제에서 주어지는 $p$가 소수가 아님에 유의하여, $60p$로 나눈 나머지를 계속해서 구한 다음 마지막에 나온 결과를 $60$으로 나눠주면 됩니다. 계산 과정 중 long long의 범위를 넘는 수가 나올 수 있으므로 __int128 등을 사용해야 합니다.
문제 3: BOJ #12748. 색칠 공부(Large)
요약
정$n$각형의 꼭지점을 $k$개의 색으로 칠하려고 합니다. 정$n$각형을 돌리거나 뒤집거나, 두 색 $X$와 $Y$를 선택해 두 색을 반전시키는 과정을 유한 번 반복해서 같은 모양이 되면 같은 색칠로 간주합니다. 이때 서로 다른 색칠의 가짓수를 구하는 문제입니다.
풀이
위의 문제들을 풀 때처럼 색칠하는 방법을 $X$, 돌리고 뒤집고 색을 반전하는 것을 $G$라 합시다. 좀더 구체적으로, $x \in X$를 $(v, c)$ 순서쌍들의 집합으로 정의합니다. $v$는 꼭짓점의 번호를, $c$는 꼭짓점에 칠해진 색을 의미합니다. 그리고 $G$를 정$n$각형의 Dihedral Group과 $k$개의 색 집합의 Symmetric Group의 direct product로 정의합니다. 즉 $G=D_n\times S_k$입니다. 연산 $* : G\times X\rightarrow X$를 $(v, c)=x\in X, (d, s)=g\in G$에 대해 $gx=(d(v), s(c))$로 정의합니다. 예를 들어, 주어진 $x\in X, g\in G$에 대해 $gx$를 계산한 결과를 그림으로 나타내면 다음과 같습니다.
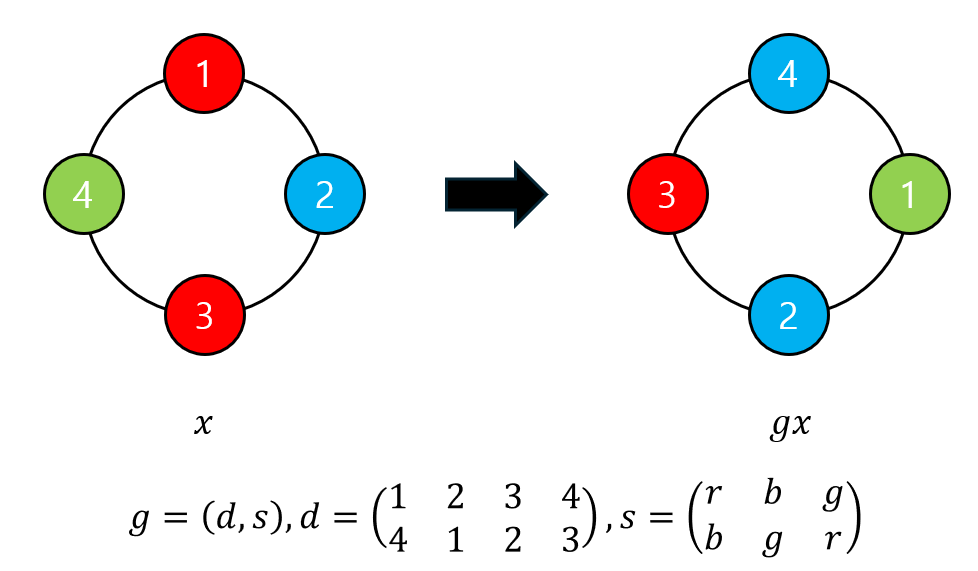
각각의 $g \in G$에 대해 $gx=x$를 만족하는 $x$의 개수를 계산해 봅시다. 색을 반전시키는 과정 없이 돌리고 뒤집는 과정만 있다면 Dihedral Group의 한 원소의 각 cycle이 모두 같은 색으로 칠해지기만 하면 됩니다. 그러나 색을 반전시키는 과정이 추가되었으므로 어디에 어떤 색이 칠해져야 할지를 추가적으로 고려해야 합니다.
$d\in D_n$의 한 사이클을 $(d_1, d_2, \cdots, d_m)$이라고 합시다. 그리고 이들에 칠해진 색을 $(c_1, c_2, \cdots, c_m)$라고 합시다. $d$에 의해 $d_1$은 $d_2$로, $d_2$은 $d_3$으로, $\cdots$, $d_m$은 $d_1$으로 이동하게 됩니다. 이때 이동하기 전과 같은 $(v, c)$ 쌍을 유지하기 위해 $c_1$은 $c_2$로, $c_2$는 $c_3$으로, $\cdots$, $c_m$은 $c_1$으로 바뀌어야 합니다. 따라서 $(c_1, c_2, \cdots, c_m)$ 또한 사이클을 이뤄야 하고 $c_i$는 $s\in S_k$의 길이가 $m$의 약수인 사이클에 포함될 때만 사이클을 이룹니다. 그리고 $c_1$이 결정되면 나머지는 사이클의 순서대로 결정되므로 $c_i$를 칠하는 가짓수는 $s$에서 길이가 $m$의 약수인 사이클에 포함된 원소의 개수입니다.
이제 모든 $(d, s)\in G$에 대해 다음을 반복하고 3에서 얻은 값을 모두 합하면 됩니다.
- $d$, $s$를 사이클로 분할한다.
- $d$의 사이클 중 하나의 길이가 $m$일 때, 모든 $m$의 약수 $i$에 대해 ($s$의 길이 $i$인 사이클의 수)$\times i$의 합을 구한다.
- $d$의 모든 사이클에 대해 2에서 구한 값을 모두 곱한다.
그러나 $\vert D_n\vert=2n, \vert S_k\vert=k!$으로 모든 원소에 대해 반복하기에는 $\vert G\vert$가 너무 큽니다. 그러므로 각 Group의 원소를 공통된 특징에 따라 분류해야 합니다. 이 문제를 푸는 데 중요한 특징은 사이클로 분할했을 때 각 사이클들의 크기이므로, 이에 따라 분류하겠습니다.
먼저 $S_k$를 보겠습니다. 각 원소는 크기 1 이상의 disjoint한 사이클로 분할할 수 있으므로 총 $P_k$(partition number)가지로 분류됩니다. 각 분류에 속하는 원소들의 개수는 $1$부터 $k$를 각 크기의 그룹으로 분류하는 경우의 수에, 각 그룹에서 순서를 정하는 경우의 수를 모두 곱하면 됩니다.
$D_n$는 크게 돌리기와 뒤집기로 나눌 수 있습니다. 돌리기에 의한 원소들을 사이클의 길이에 따라 분류하면, $i\vert n$인 모든 $i$에 대해 길이 $i$인 사이클 $\frac{n}{i}$개로 분할되는 $d\in D_n$이 $\phi(i)$(오일러 phi 함수)개 있습니다. $i$를 $1$부터 $\sqrt n$까지만 반복하면서 사이클의 길이가 $i, \frac ni$일 때를 동시에 처리하면 됩니다. 뒤집기에 의한 원소들은 $n$이 홀수일 때 길이 $2$의 사이클 $\lfloor \frac n2 \rfloor$개와 길이 1의 사이클 1개로 분할되는 $d\in D_n$ $n$개 있습니다. $n$이 짝수일 때는 길이 $2$의 사이클 $\frac n2$개로 분할되는 $\frac n2$개와, 길이 $2$의 사이클 $\frac n2-1$개와 길이 $1$의 사이클 $2$개로 분할되는 $\frac n2$개가 있습니다.
각 그룹에 속하는 원소들의 개수와 그 원소에 의한 $\vert X_g\vert$를 곱한 다음, 이들을 모두 더하면 됩니다. 마지막으로 이를 $\vert G\vert=\vert D_n\vert \vert S_k\vert$으로 나누면 답을 구할 수 있습니다. 시간복잡도는 $n$의 약수에 대한 phi 함수를 그때그때 계산하더라도 $O((kP_k+\pi(\sqrt n))d(n))$입니다. $d(n)$, $\pi(\sqrt n)$은 각각 $n$의 약수의 개수, $1$부터 $\sqrt n$까지의 소수의 개수입니다. $P_k\leq 1958, d(n)\leq 1344, \pi(\sqrt n)\leq 3401, k\leq 25$이므로 시간 제한을 통과할 수 있습니다.
참고문헌
[1] https://feog.github.io/chap1dm.pdf
[2] https://www.diva-portal.org/smash/get/diva2:324594/FULLTEXT01.pdf
[3] https://personal.math.ubc.ca/~cass/courses/m308-05b/projects/cchang/webpages/dodecahedron.html