Moving Least Squares Projection
Point Based Graphics
Point Based Graphics는 컴퓨터 그래픽스의 한 분야로, 기존의 다각형 기반으로 형상을 모델링하는 기법인 Polygon Based Graphics와 달리 점들을 사용하여 3D 객체의 표면을 표현하는 기법입니다.
각 점은 위치 뿐만 아니라 그 지점의 색상과 텍스쳐 등 다양한 속성도 가질 수 있습니다. 여기서 객체를 표현하는데 사용된 점들의 집합을 Point Cloud라고 합니다. 이 Point Cloud가 조밀할수록 더욱 세밀한 형태를 표현할 수 있습니다.

Point Based Graphics는 복잡한 형상을 기존 기법보다 더 효율적이고 자세하게 표현할 수 있다는 장점이 있습니다. 또한 3D 스캐닝 등의 기법을 통해 물리적으로 존재하는 사물에 대한 정보는 Point Cloud로 표현되기에 이를 컴퓨터 화면 속으로 옮기는데 유리합니다.
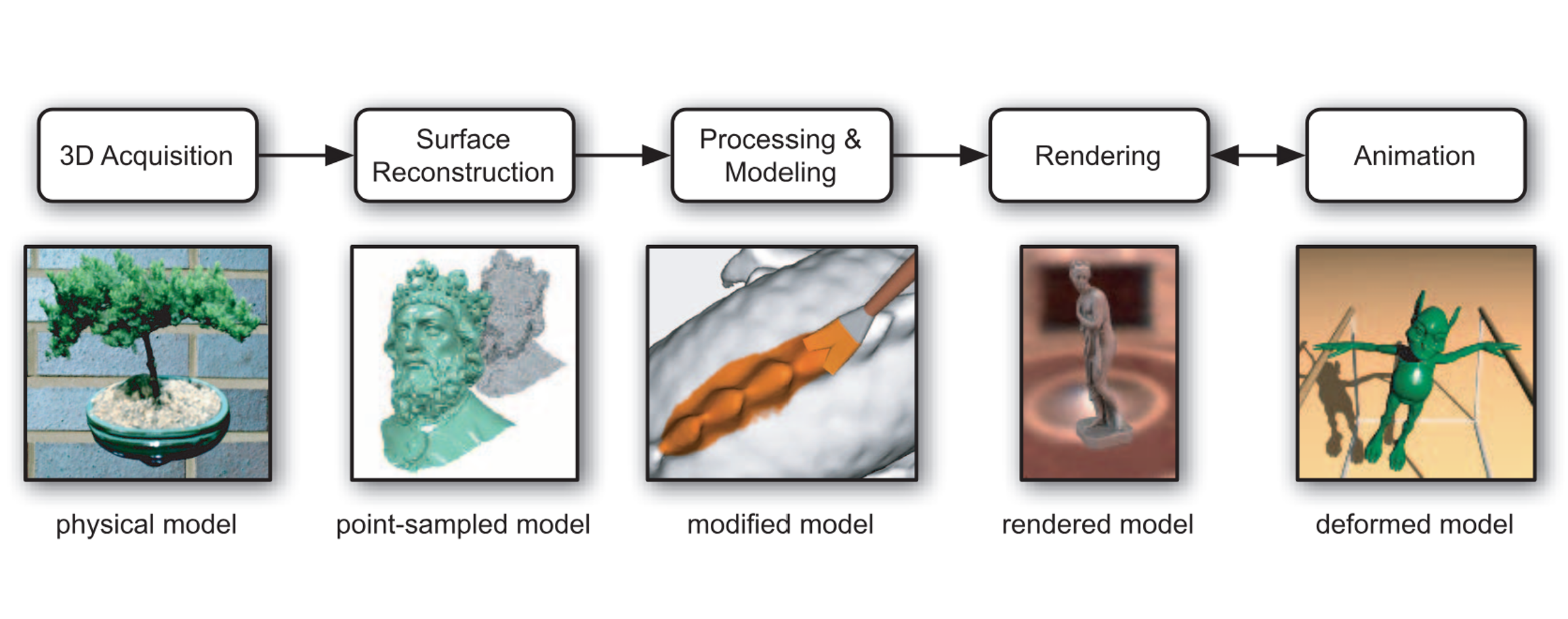
위 그림은 Point Based Graphics의 전체적인 pipeline입니다. 이 글에서는 그 중 두번째 단계인 Surface Reconstruction에 대해 다뤄보도록 하겠습니다.
Moving Least Squares Projection
Point Cloud만을 가지고 객체를 표현하는데에는 큰 한계가 있습니다. Point Cloud는 각 점의 색, 텍스쳐 정보 등에 관한 속성은 존재하지만 주변 점들과 어떠한 방식으로 연결되어 있는지에 대한 정보가 결여되어 있기 때문입니다. 또한, Point Cloud는 기본적으로 물리적인 객체에 대한 측정으로 얻어지는 정보이기에 매끈한 면이더라도 노이즈가 생기기 마련입니다. 따라서 Point Cloud으로부터 역으로 측정한 객체의 표면을 유추하는 과정이 필요합니다. 이때 사용하는 기법이 Moving Least Squares Projection (MLS Projection)입니다.
MLS Projection의 목표는 Point Cloud가 주어졌을 때, 임의의 점 $p$에서 그 Point Cloud로부터 정의되는 가상의 표면으로 사영시키는 함수 $P_m$을 유도하는 것입니다. 이렇게 $P_m$을 구해놓고 나면, 다양한 위치의 점을 Sampling한 후 $P_m$을 통해 사영시켜 가상의 표면에 점들이 찍힐 것이고, 이 점들을 통해 객체의 표면을 Reconstruct할 수 있습니다.
이를 general하게 써보면 다음과 같습니다.
$d$차원 공간에서 $N$개의 점으로 구성된 점들의 집합 $R=\lbrace r_i\rbrace_{0\leq i\lt N}$와 임의의 점 $p$가 주어졌을 때 $R$을 표현하는 어떤 $d-1$차원 면 $S$ 위로의 Projection Operator $P_m$를 구하시오.
Step 1 - Local Approximating Hyperplane
먼저, $p$ 주위의 $\lbrace r_i\rbrace$들의 위치를 approximate하는 면 $H$를 구할 것입니다. 임의의 면은 그 normal vector $a$를 사용해 다음과 같이 표현할 수 있습니다.
\[H= \{x\,\vert\, a\cdot x-D=0, x\in \mathbb{R}^d, \Vert a\Vert =1\}\]여기서 추가적으로 점 $p$의 $H$ 위로의 사영 $q$를 정의하겠습니다. 이를 다르게 표현하면 다음과 같습니다.
\[q=p+ta, t\in \mathbb{R}\]이제 다음의 식을 locally minimize하는 $H$를 구할 것입니다.
\[\sum\limits_{r_i \in R}(a\cdot r_i-D)^2\theta(\Vert r_i-q\Vert )=\sum\limits_{r_i \in R}(a\cdot(r_i-p-ta))^2\theta(\Vert r_i-p-ta\Vert)\]다른 말로 하면, 위의 식을 locally minimize하는 어떤 스칼라 $t$와 $d$차원 방향벡터 $a$를 구해야 합니다. 여기서 $\theta$는 weight function으로 일반적으로 $\theta(x)=e^{-x^2/h^2}$를 사용합니다. $h$는 $R$ 위의 점들 사이의 평균 거리입니다.
혹자는 위의 weight function에서 왜 $\Vert r_i-p\Vert$ 대신 $\Vert r_i-q\Vert$를 썼는지 의문이 들 수 있습니다. 이는 최종적으로 구하는 $P_m$이 Projection Operator이도록 하는 장치로, 이후 다시 짚어보도록 하겠습니다.
위를 locally minimize하는 $(a, t)$ 가 여러 개 있는 경우, 그 중에서 $\vert t\vert$의 값이 가장 작은 쌍을 선택합니다.
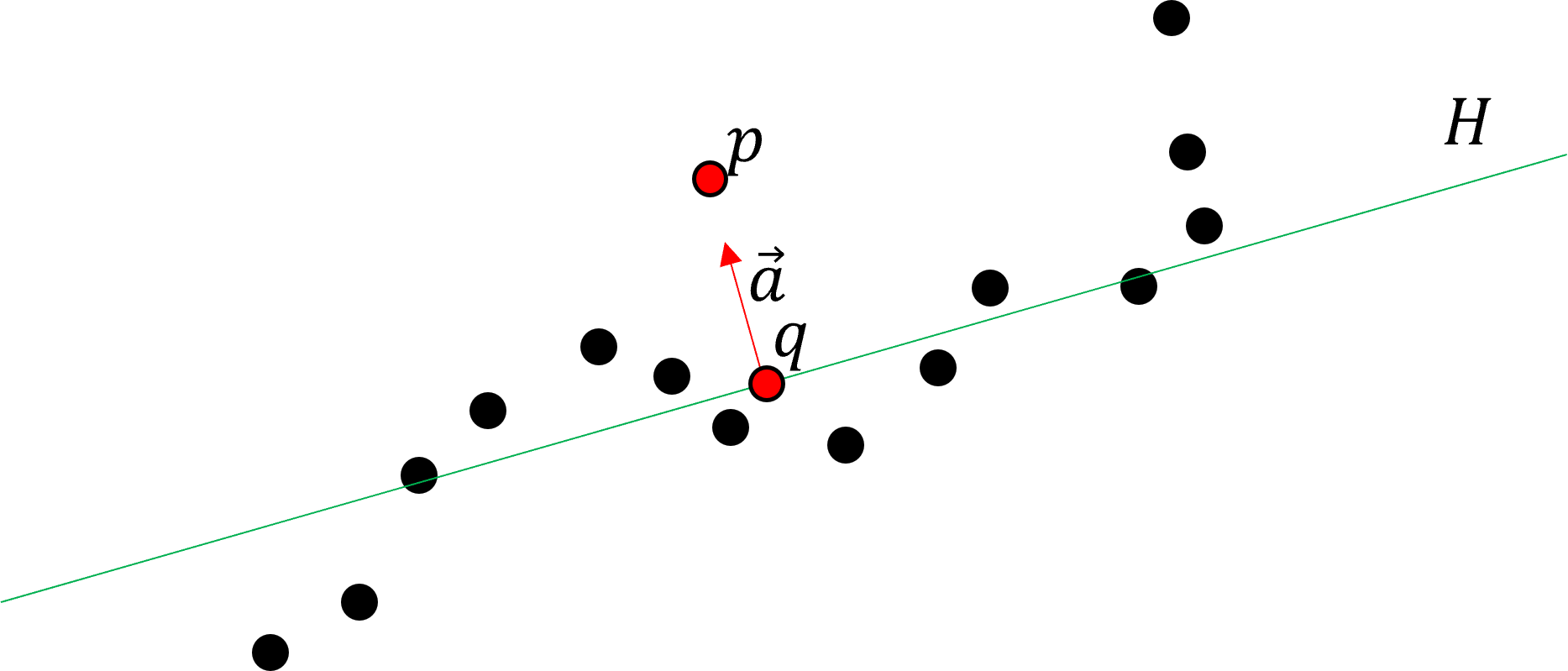
위 그림은 $d=2$인 경우의 예시입니다. 이때 $H$는 직선의 형태로 그려집니다.
이 과정을 통해 구한 $a$와 $q=p+ta$를 각각 $A(p)$, $Q(p)$라 하겠습니다.
Step 2 - MLS Projection
$\lbrace x_i\rbrace_{0\leq i\lt N}$를 Step 1에서 구한 평면 $H$에 대한 $\lbrace r_i\rbrace_{0\leq i\lt N}$의 사영이라 하겠습니다. 또한 $f_i=r_i\cdot a-D$이라 하여, $H$로부터 $r_i$의 거리를 정의하겠습니다.
이제, 평면 $H$와 그 normal $a$로 이루어지며, 원점이 $q$에 위치한 orthonormal coordinate를 잡습니다.
그 좌표계 위에서 Square error을 최소화하는 어떤 다항식 $P$를 구합니다. 구체적으로, 다음의 식을 최소화해아합니다.
\[\sum\limits_{0\leq i \lt N}(P(x_i)-f_i)^2\theta(\Vert r_i-q\Vert)\]여기서 $P$는 $d-1$차원의 다항식이며, 이는 기존의 Polynomial Regression을 통해 구할 수 있습니다.
마지막 단계로, $P_m(p)=q+P(0)a$ 으로 정의합니다. 이 $P_m$이 우리가 구하고자 한 Projection Operator입니다.
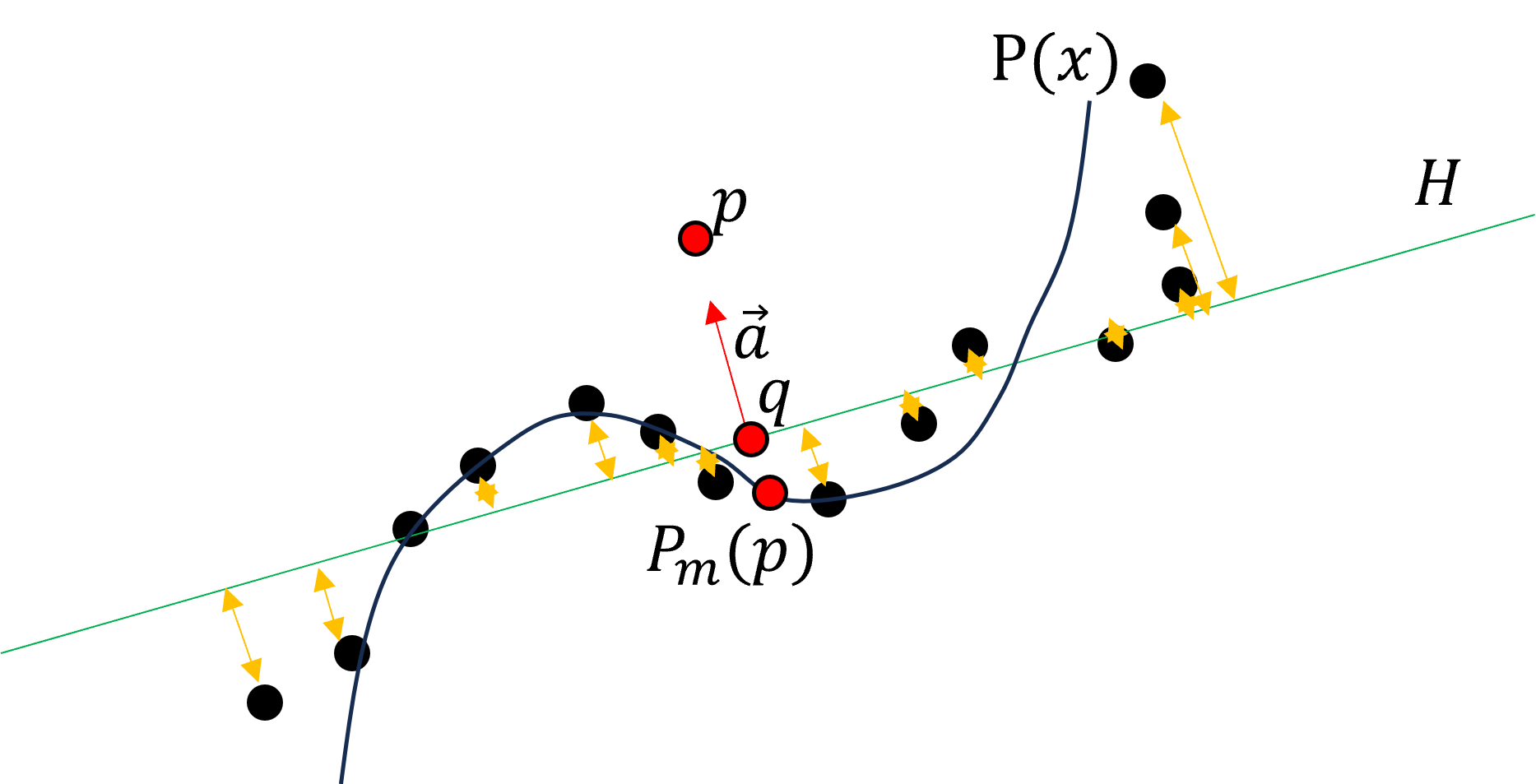
위 그림은 $d=2$인 경우에 3차함수를 이용한 Regression의 결과와 MLS Projection의 결과를 나타낸 예시입니다.
Sanity Check
위 방식이 진짜로 Projection인지 확인이 필요합니다. 즉, $P_m(p)=P_m(P_m(p))$인지 확인해야 합니다.
Step 2에서 최적화하는 식을 보면, 이 식은 $H$만 정해졌다면 $p$와 무관하다는 사실을 알 수 있습니다. 따라서, $p$와 $P_m(p)$에 대한 Local Approximating Hyperplane $H$가 같은지만 확인하면 됩니다.
또한 Step 1에서 $(a, t)$가 점 $p$에 대해 식을 최소화했다고 가정한다면, $(a, t-s)$는 점 $p’=p+sa$에 대해 식을 최소화한다는 사실을 알 수 있습니다. 여기서 가중치 함수로 $\theta(\Vert r_i-p\Vert)$ 가 아닌 $\theta(\Vert r_i-q\Vert)$ 를 채택한 이유가 나옵니다. 만약 $\theta(\Vert r_i-p\Vert)$를 선택했다면 위 명제는 성립하지 않습니다.
이에 의해 $q=p+ta$이므로, $A(q)=A(p)$이며 $Q(q)=(p+ta)+(t-t)a=q=Q(p)$ 입니다.
추가로 $P_m(p)=q+P(0)a=p+ta+P(0)a=p+(t+P(0))a$ 이므로 $A(P_m(p))=A(p)$ 이고,
$Q(P_m(p))=P_m(p)+(t-(t+P(0)))a=q+P(0)a-P(0)a=q=Q(p)$ 입니다.
따라서 $p$와 $P_m(p)$로부터 유도되는 $H$가 같으므로, $P_m(p)=P_m(P_m(p))$를 만족합니다. 이제 우리는 MLS Projection으로부터 유도된 MLS Hypersurface를 다음과 같이 적을 수 있습니다 :
\[S=\{x|P_m(x)=x, x\in \mathbb{R}^d\}\]Conclusion
우리는 주어진 점 집합에 대해 MLS Projection을 통해 하나의 unique한 hypersurface를 구할 수 있게 되었습니다. 비록 이 hypersurface는 측정의 noise도 줄이고 표면도 smooth하지만 한계도 분명히 있습니다.
첫째, 원래 측정한 물체의 뾰족한 부분(sharp feature)이 제대로 표현되지 않고 뭉툭한 형태로 구해집니다. 둘째, Projection 1회당 드는 연산량이 $O(N)$정도로, 원래 점의 개수가 충분히 작을 때는 상관없지만 대형 모델들에 대해 전체 hypersurface를 그리려 하면 상당히 많은 시간이 소요될 수 있습니다.
첫번째 한계점은 Step 1에서의 Hyperplane 대신 구와 같은 곡률이 있는 면을 사용함으로써 해결할 수 있음이 알려져 있고, 두번째 한계점은 약간의 근사를 통해 1회당 $O(logN)$ 수준의 연산으로 최적화할 수 있습니다. 추후 글에서는 이 방법에 대해 알아보도록 하겠습니다.
Reference
[Gross, Markus, and Hanspeter Pfister. Point-Based Graphics. Elsevier/Morgan Kaufmann, 2007.]
https://cgl.ethz.ch/publications/tutorials/eg2002
[Levin, David. “Mesh-independent surface interpolation.” Geometric modeling for scientific visualization. Springer Berlin Heidelberg, 2004.]