Ladder Decomposition
개요
트리의 Ladder Decomposition은 Heavy-Light Decomposition과 유사하게, 트리를 경로들의 집합으로 분해하는 기법이다. 이번 글에서는 Ladder Decomposition의 정의와 알고리즘, 그리고 이를 응용해서 풀 수 있는 문제에 대해 알아보고자 한다.
정의
Ladder Decomposition를 한 문장으로 줄여 말하면 ‘HLD인데, subtree의 크기가 아니라 높이를 대신 본 것’ 이다.
구체적으로, Ladder Decomposition은 다음과 같은 알고리즘으로 구할 수 있다.
먼저 $h(u)$ 를 정점 $u$를 루트로 하는 서브트리의 높이라 정의하자.
루트부터 DFS를 실행하면서 정점 $v$에 도달 했을 때, $v$의 자식들이 $c_1$, $c_2$, …, $c_k$이며, $h(c_1)\geq h(c_2)\geq … \geq h(c_k)$ 를 만족한다 가정하자. $c_1$번 정점의 chain은 $v$의 것과 연결되게 하고, 나머지 정점들은 자기 자신을 꼭대기로 하는 새로운 chain을 가진다.
이제 모든 chain에 대해, 그 길이가 len이라면 chain의 현재 꼭대기 정점으로부터, 부모 방향으로 길이 len만큼을 추가로 확장하며, 이를 ladder라 한다.
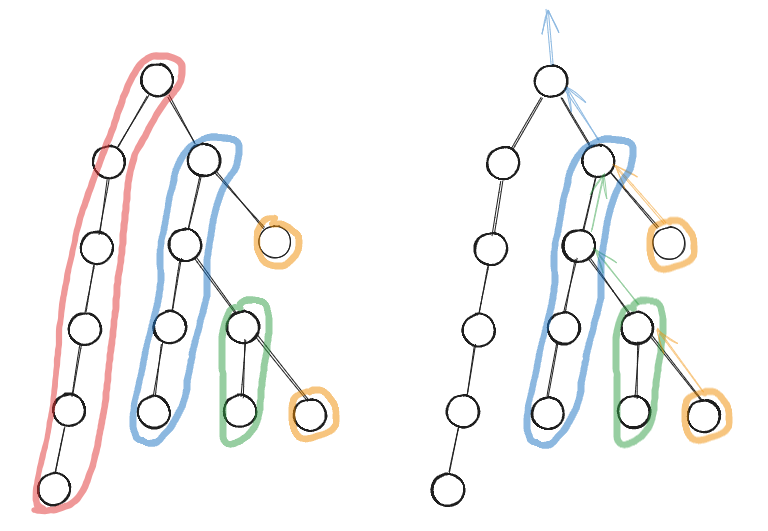
이렇게 해도 문제가 안될 것이, 어차피 모든 chain들의 길이의 합은 $N$이다. 따라서 각 chain의 ladder까지 고려했을 때도 그 길이의 합은 $2N$이다.
주의할 점으로는, ladder부분은 여러번 중복될 수 있다는 것이다. 즉 update 쿼리에 적용하기는 쉽지 않지만, binary lifting과 함께 특히 kth-ancestor 문제를 더욱 효율적으로 해결할 수 있는 구조이다.
kth-ancestor
Ladder Decomposition과 binary lifting을 이용해 kth-ancestor를 $O(NlogN)$ 전처리를 통해 $O(1)$에 구할 수 있다.
먼저, Ladder Decomposition을 실행하고 Binary Lifting을 위한 sparse table을 만든다.
정점 $u$의 $k$-th ancestor를 구한다 가정하자.
$2^w \leq k$인 최대의 $w$를 구하자. Binary Lifting을 이용해 $2^w$ 칸 위의 정점 $v$를 구한다.
이제, $v$로부터 $k-2^w$칸 위의 점 $w$를 구해야 한다. 중요한 관찰은, $v$가 속해있는 chain의 길이는 최소 $2^w$이라는 것이다. $v$라는 정점이 애초에 $u$에서 $2^w$ 칸 올라간 정점이며, ladder decomposition의 정의에 의해 $v$의 chain은 $h(v)$ 이상의 길이를 가질 것이기 때문이다.
그런데, $v$의 ladder도 마찬가지로 $h(v)$ 이상의 길이를 가지게 된다. 이는 $v$에서 그 ladder까지 고려했을 때 반드시 $k-2^w$칸 위의 점까지 포함된다는 것을 보장한다.
위 알고리즘의 병목은 binary lifting에서의 전처리 과정이다. 이 또한 해결할 수 있는 방법이 많이 연구되어 있으며, Four Russian Method 등을 이용하여 $O(N)$ 수준으로의 개선이 가능하나 상수로 인해 이론적인 영역에서만 가능한 최적화이다.
Path Max/Min Query
위에서 언급한 kth-ancestor 로직을 사용하면, Path Max/Min Query 또한 O(1)에 해결할 수 있다. 전처리는 마찬가지로 $O(NlgN)$ 혹은 $O(N)$에 가능하다.
정점 $u$와 $v$ 사이의 LCA는 Cartesian Tree와 O(1) RMQ를 이용하여 O(1)에 구할 수 있음이 알려져 있다. (관련 글 링크)
여기에 더해, 각 chain/ladder별로 O(1)에 RMQ를 해결할 수 있도록 전처리를 해줄 수 있다. (관련 글 링크)
이 두 로직을 합치면, 직선 뿐만 아니라 정적인 트리에서도 O(1)에 Path Max/Min Query를 해결할 수 있다.