Dulmage-Mendelsohn Decomposition (Part 1)
개요
이 글에서는 Dulmage-Mendelsohn Decomposition의 개념과 성질을 소개하고 이를 구하는 방법에 대해서 다룹니다. Dulmage-Mendelsohn Decomposition의 코드와 PS에서의 활용은 다음으로 이어지는 글에서 다루겠습니다.
사전 지식으로 이분 매칭과 SCC를 알고 있다고 가정하고 진행하겠습니다.
Dulmage-Mendelsohn Decomposition(DM 분해)는 이분 그래프의 모든 최대 매칭의 구조를 알아내기 위해서 정점 집합을 여러 개의 부분집합들로 unique하게 분할하는 방법입니다.
구체적으로 예를 들면, DM 분해를 사용해서 아래와 같은 질문들에 대해 빠르게 답변할 수 있습니다.
-
주어진 이분 그래프의 각 정점 $u$에 대해,
-
모든 최대 매칭에서 $u$가 사용되는가?
-
$u$를 사용하는 최대 매칭이 존재하는가?
-
어떤 최대 매칭에서도 $u$가 사용되지 않는가?
-
-
주어진 이분 그래프의 각 간선 $e$에 대해,
-
모든 최대 매칭에서 $e$가 사용되는가?
-
$e$를 사용하는 최대 매칭이 존재하는가?
-
어떤 최대 매칭에서도 $e$가 사용되지 않는가?
-
DM 분해는 Coarse Decomposition과 Fine Decomposition 두 개의 파트로 이루어져 있습니다.
Coarse Decomposition
이분 그래프 $G=(L \sqcup R,E)$의 아무런 최대 매칭 $M$이 주어지면, $M$을 이용해서 정점 집합 $L \sqcup R$을 아래 조건을 만족하는 세 개의 disjoint한 정점 부분집합 $\mathcal{E}, \mathcal{O}, \mathcal{U}$ (even, odd, unreachable)로 분할할 수 있고, 이를 Coarse Decomposition이라 부릅니다.
-
매칭되지 않은 정점으로부터 출발하는 짝수 길이의 alternating path를 통해 $u$에 도달할 수 있다면 $u \in \mathcal{E}$입니다.
-
매칭되지 않은 정점으로부터 출발하는 홀수 길이의 alternating path를 통해 $u$에 도달할 수 있다면 $u \in \mathcal{O}$입니다.
-
매칭되지 않은 정점으로부터 출발하는 alternating path를 통해 $u$에 도달할 수 없다면 $u \in \mathcal{U}$입니다.
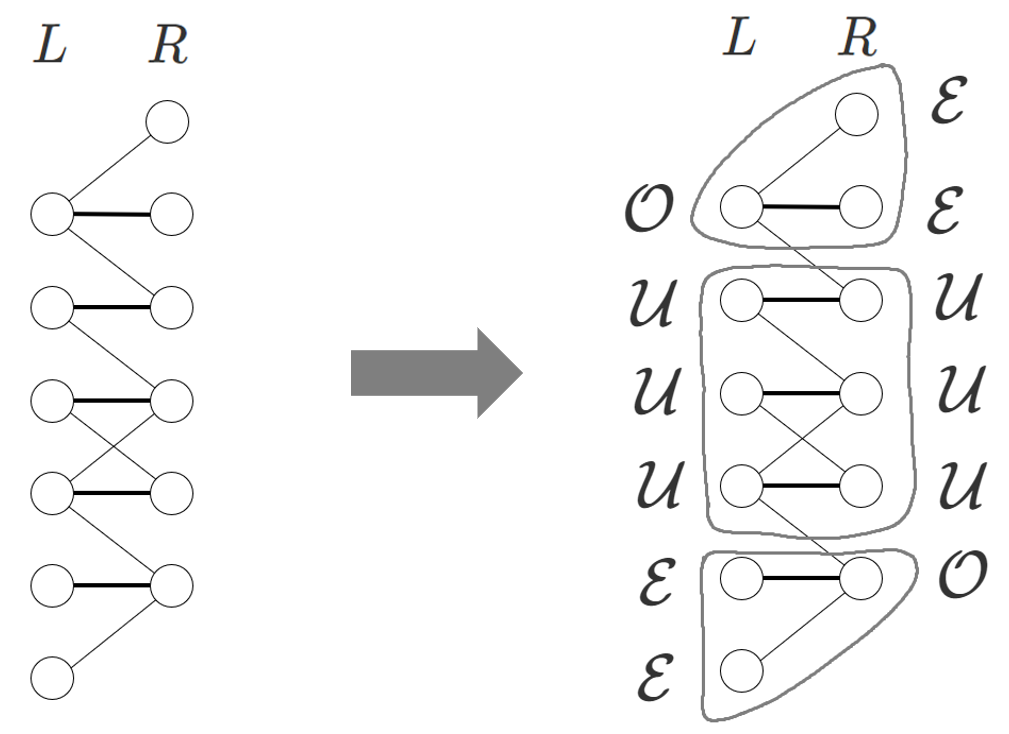
위 그림은 Coarse Decomposition을 수행한 예시입니다.
성질
Coarse Decomposition은 다음과 같은 성질을 갖습니다.
-
각 정점은 $\mathcal{E}, \mathcal{O}, \mathcal{U}$ 중에 정확히 하나에만 속합니다.
-
$M$을 어떻게 선택하는지에 관계없이 $\mathcal{E}, \mathcal{O}, \mathcal{U}$는 유일하게 결정됩니다.
-
$E$의 간선들은 $\mathcal{O}-\mathcal{E}, \mathcal{O}-\mathcal{O}, \mathcal{O}-\mathcal{U}, \mathcal{U}-\mathcal{U}$ 중 하나로 분류할 수 있습니다.
-
$M$의 간선들은 $\mathcal{O}-\mathcal{E}, \mathcal{U}-\mathcal{U}$ 중 하나로 분류할 수 있습니다.
-
각 정점 $u$를 다음과 같이 분류할 수 있습니다.
-
$u \in \mathcal{O}$ 또는 $u \in \mathcal{U}$라면, 모든 최대 매칭에서 $u$가 사용됩니다.
-
$u \in \mathcal{E}$이면서 $u$가 고립되어 있지 않다면, $u$를 사용하는 최대 매칭과 사용하지 않는 최대 매칭이 둘 다 존재합니다.
-
$u \in \mathcal{E}$이면서 $u$가 고립되어 있다면, 어떤 최대 매칭에서도 $u$가 사용되지 않습니다.
-
-
따라서 $\lvert \mathcal{O} \rvert + \lvert \mathcal{U} \rvert / 2$가 최대 매칭의 크기가 됩니다.
Fine Decomposition
Coarse Decomposition에서 $\mathcal{U}$를 추가적으로 분할해서 더 많은 정보를 얻을 수 있습니다.
먼저, 정점 집합이 $\mathcal{U}$인 새로운 방향 그래프 $G’$를 생성합니다. $a \in L, b \in R$인 각 간선 $(a,b) \in E$에 대해,
-
$(a,b) \in M$이라면 $G’$에 양방향으로 $a \rightarrow b, b \rightarrow a$를 모두 추가합니다.
-
$(a,b) \not \in M$이라면 $G’$에 단방향으로 $a \rightarrow b$를 추가합니다.
이렇게 만들어진 $G’$에서 SCC들을 모두 구하고, $\mathcal{U}$를 SCC 단위로 분할하면 Fine Decomposition을 얻을 수 있습니다.

위 그림은 Fine Decomposition을 수행한 예시입니다.
성질
Fine Decomposition은 다음과 같은 성질을 갖습니다.
-
$M$을 어떻게 선택하는지에 관계없이 $\mathcal{U}$의 분할은 유일하게 결정됩니다.
-
서로 다른 그룹끼리는 최대 매칭을 구할 때 독립적으로 생각해도 됩니다.
-
각 간선 $e$를 다음과 같이 분류할 수 있습니다.
-
$e$의 양 끝점이 속한 그룹이 서로 같으면서 그룹의 크기가 정확히 2라면, 모든 최대 매칭에서 $e$가 사용됩니다.
-
$e$의 양 끝점이 속한 그룹이 서로 같으면서 그룹의 크기가 2 초과라면, $e$를 사용하는 최대 매칭과 사용하지 않는 최대 매칭이 둘 다 존재합니다.
-
$e$의 양 끝점이 속한 그룹이 서로 다르다면, 어떤 최대 매칭에서도 $e$가 사용되지 않습니다.
-
Dulmage-Mendelsohn Decomposition
지금까지의 내용을 종합하면 아래와 같습니다.
이분 그래프 $G=(L \sqcup R,E)$가 주어지면, $G$의 DM 분해는 아래의 조건들을 모두 만족하는 $\lbrace (L_0, R_0), (L_1, R_1), \cdots, (L_{K+1}, R_{K+1}) \rbrace$을 반환합니다. $(K \geq 0)$
-
$L = L_0 \sqcup L_1 \sqcup \cdots \sqcup L_{K+1}$
-
$R = R_0 \sqcup R_1 \sqcup \cdots \sqcup R_{K+1}$
-
$\lvert L_0 \rvert < \lvert R_0 \rvert$ 또는 $L_0 = R_0 = \emptyset$이 성립합니다.
-
$\lvert L_{K+1} \rvert > \lvert R_{K+1} \rvert$ 또는 $L_{K+1} = R_{K+1} = \emptyset$이 성립합니다.
-
$1 \leq i \leq K$에서 $\lvert L_i \rvert = \lvert R_i \rvert > 0$이 성립합니다.
-
$G$의 모든 최대 매칭에서 $L_0, R_{K+1}, L_i, R_i (1 \leq i \leq K)$ 내의 모든 정점이 사용됩니다.
-
$a \in L, b \in R$인 각 간선 $(a,b) \in E$에 대해, $a \in L_i, b \in R_j$라면 $i \leq j$가 성립합니다. 이 때 $i = j$인 경우에만 $G$에서 $(a,b)$를 사용하는 최대 매칭이 존재합니다.
위 내용은, 모든 간선의 방향을 $L \rightarrow R$로 주었을 때 위상정렬된 순서대로 $(L_i, R_i)$들의 순서를 결정했다는 뜻입니다. 위상정렬 순서가 여러가지일 수 있음을 제외하면 $G$의 DM 분해는 유일하게 결정됩니다.
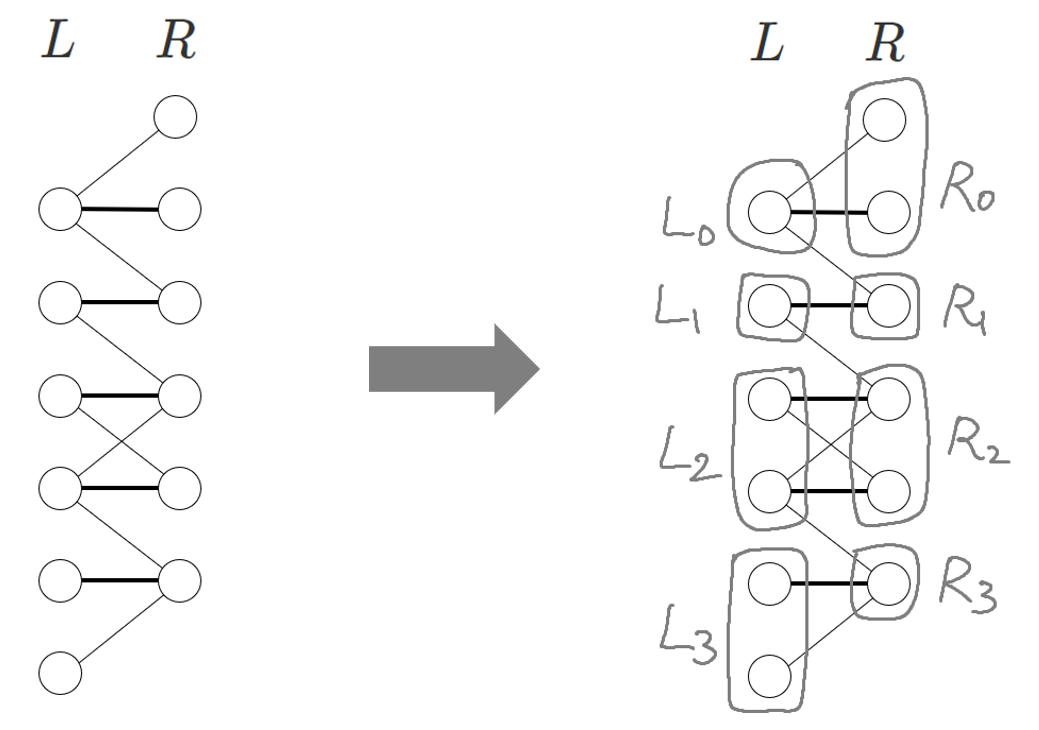
위 그림은 DM 분해를 수행한 예시입니다.
구현
Coarse Decomposition과 Fine Decomposition 파트에 적힌 내용을 차례대로 구현하면 됩니다.
-
$G$의 최대 매칭 $M$을 아무거나 하나 구합니다.
-
$M$에서 사용되지 않은 정점들을 시작점으로 해서, 짝수 길이의 alternating path를 통해 방문할 수 있는 정점들과 홀수 길이의 alternating path를 통해 방문할 수 있는 정점들을 구합니다. 이를 이용해 $L_0, R_0, L_{K+1}, R_{K+1}$을 구성합니다.
-
남은 정점들을 양 끝점으로 하는 간선들에 대해서, $M$에서 사용되지 않은 간선이라면 단방향으로 $a \rightarrow b$를 추가하고, $M$에서 사용된 간선이라면 양방향으로 $a \rightarrow b, b \rightarrow a$를 모두 추가한 새로운 방향 그래프를 생성합니다.
-
새로운 방향 그래프를 SCC들로 분할하고 위상 정렬을 수행해서 $L_1, R_1, \cdots, L_K, R_K$를 구성합니다.
최대 매칭을 구하는 과정에서 가장 큰 병목이 일어나므로, 최종 시간복잡도는 Kuhn’s Algorithm을 사용해서 이분 매칭을 구했을 때 $O(VE)$, Hopcroft-Karp Algorithm을 사용해서 이분 매칭을 구했을 때 $O(E \sqrt V)$가 됩니다.